元で,関数y = ax2 のグラフとして学習する。 放物線の特徴として,原点を通り,y 軸につ いて対称な滑らかな曲線であることが挙げら れる。本授業はこれらの特徴をもとに,写真 1,写真2,写真3の曲線のうち,どの曲線が 放物線であるかを判断する。3/4時 ・ 関数 y = a x 2 ( a <0)のグラフの特徴をとらえることができる。 ・ 関数 y = a x 2 ( a <0)のグラフをかくことができる。 グラフ用紙に関数 y = x 2 のグラフをかく。 (※グラフ用紙を準備する。 ) 本時の学習内容「関数 y = a x 2 ( a <02次関数のグラフ χの2乗に比例する関数 問題1 正解1 解説1 問題2 正解2

Yax2 Y Descubre Como Resolverlo En Qanda
Y=ax2 グラフ 特徴
Y=ax2 グラフ 特徴-二次関数 y=ax2bxc のグラフの特徴について理解し、与えられた条件から、 二次関数の式を求めることができる。 ・定期考査の得点 ・授業態度 ・ 課題等の提出状況 ・基本事項を活 用,応用できるか などを総合的に考える。 3 2章 2次関数本時で育てたい資質・能力 ・これまでに学習したことを基にグラフの特徴を予想すること ・グラフをかくことを通して,数学的にグラフの特徴を表現すること 対象 中学3年 種別 特集 仕様 全4ページ




2次関数 Y Ax Qのグラフの書き方 グラフの平行移動 数学i By ふぇるまー マナペディア
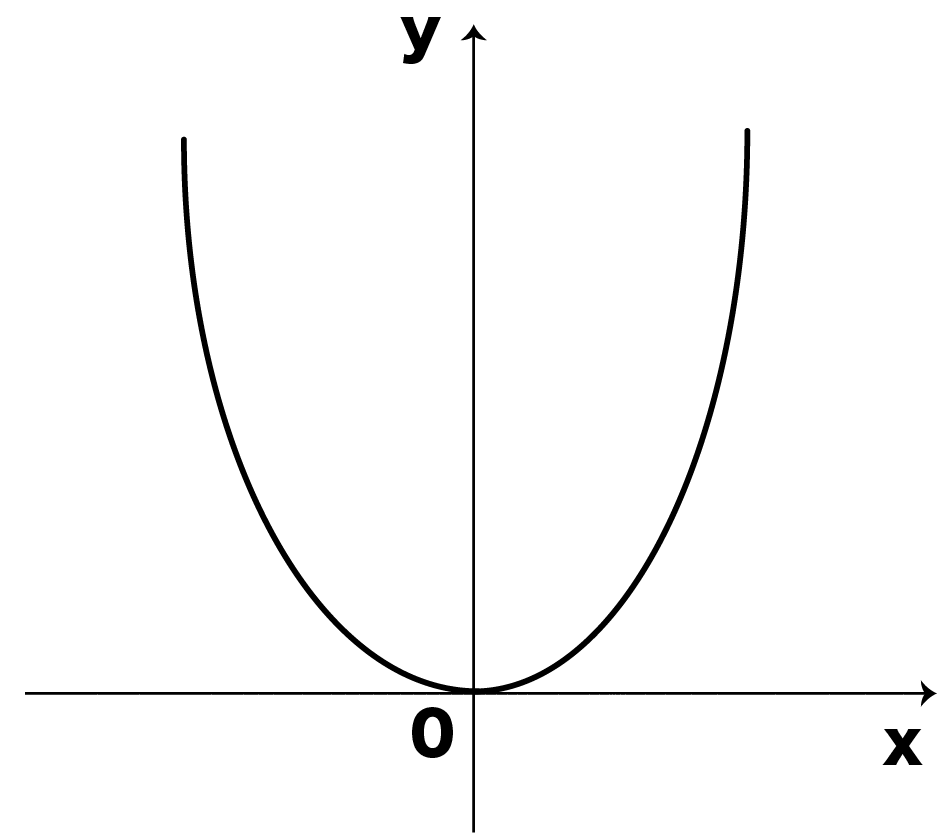
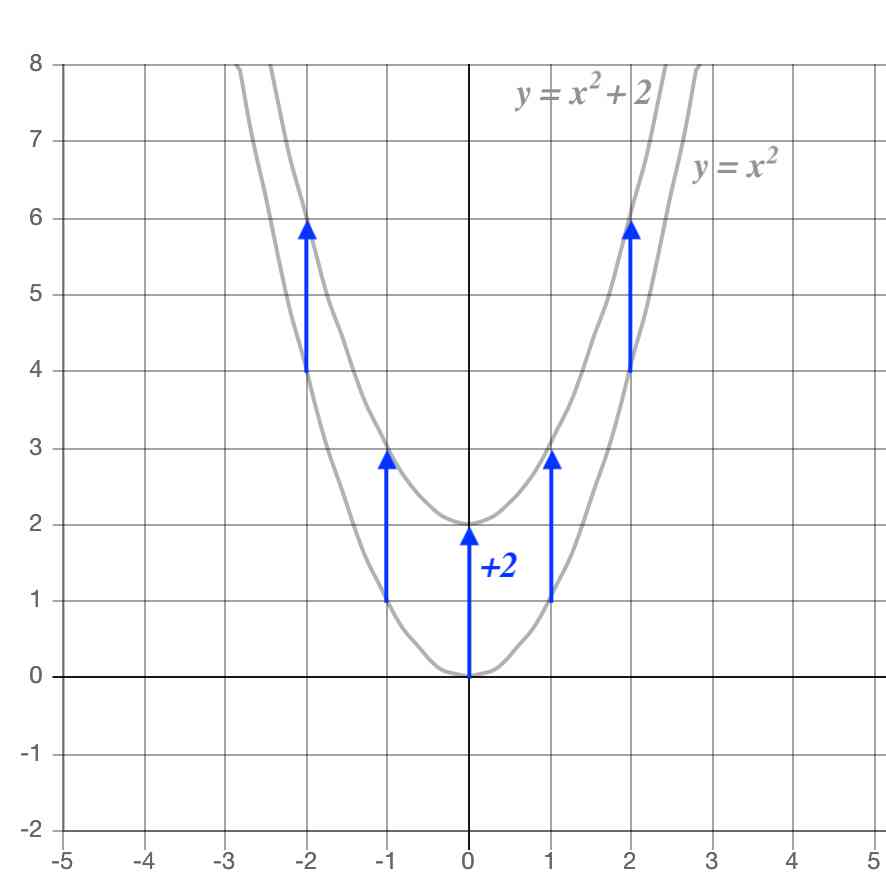
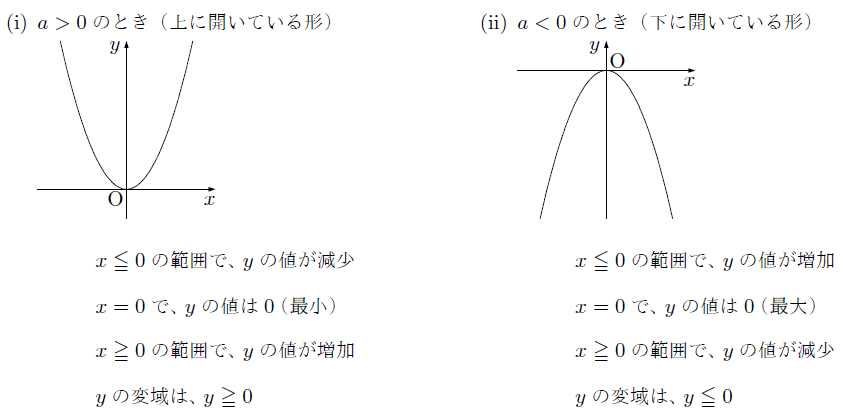
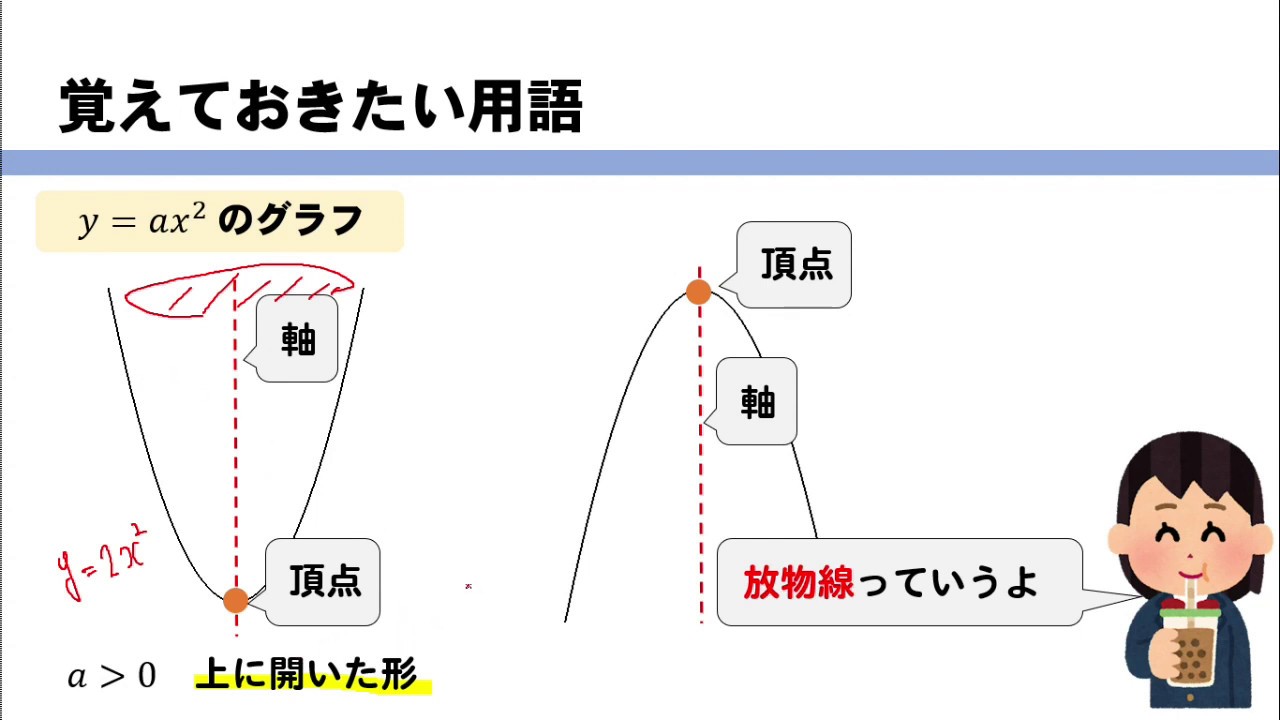
Y=ax2 を取り扱い、変化の割合やグラフの特徴など関数の理解を一層深めていくことになる。 既習事項の比例や1次関数のグラフが直線になるのと異なり、グラフが曲線になることから、 理解が困難な部分もあるため、十分な配慮が必要であると考える。Y=ax 2 のグラフは,右図のような形をしており,「物を投げたときにできる曲線」になっているので,放物線と呼ばれます. y=ax 2 のグラフは, a>0のとき,上に開いています.(谷形です.)表,式,グラフの特徴から関数y=ax2の特徴を見い出し,その特徴を根拠にした説明をさ せる。 思-② 課題解決のための見通しを持たせ,共有する場を設定する。 思-③ グループ内で全員が表・式・グラフ等を用いて考えを発表する場を設定する。
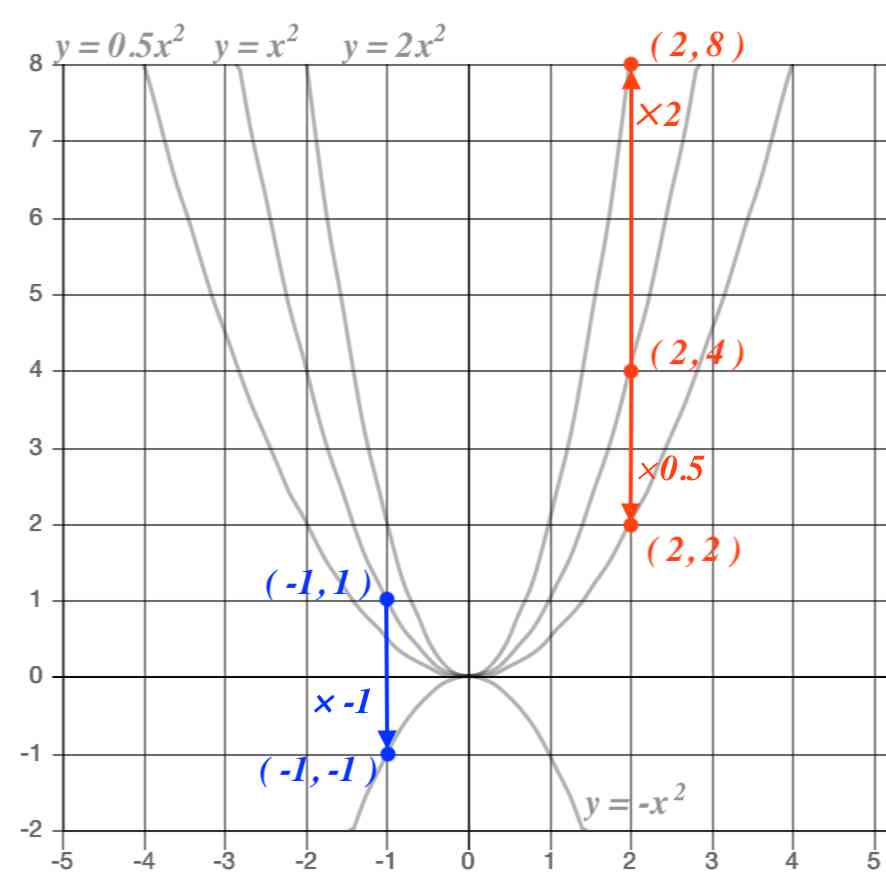
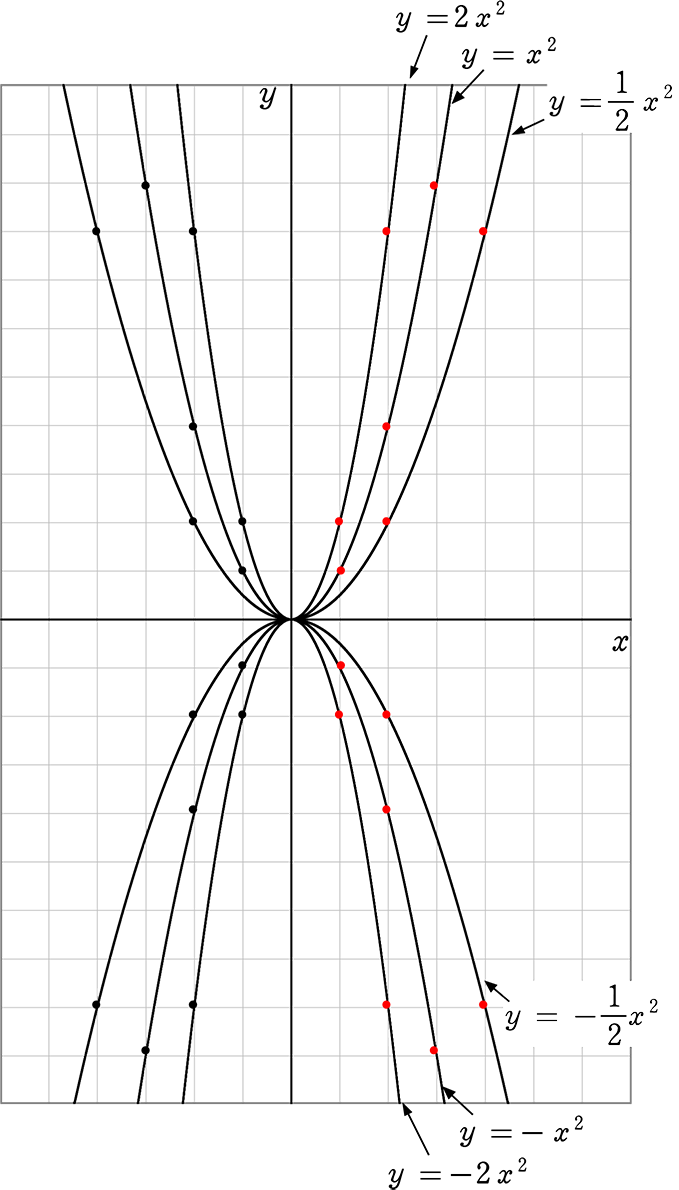
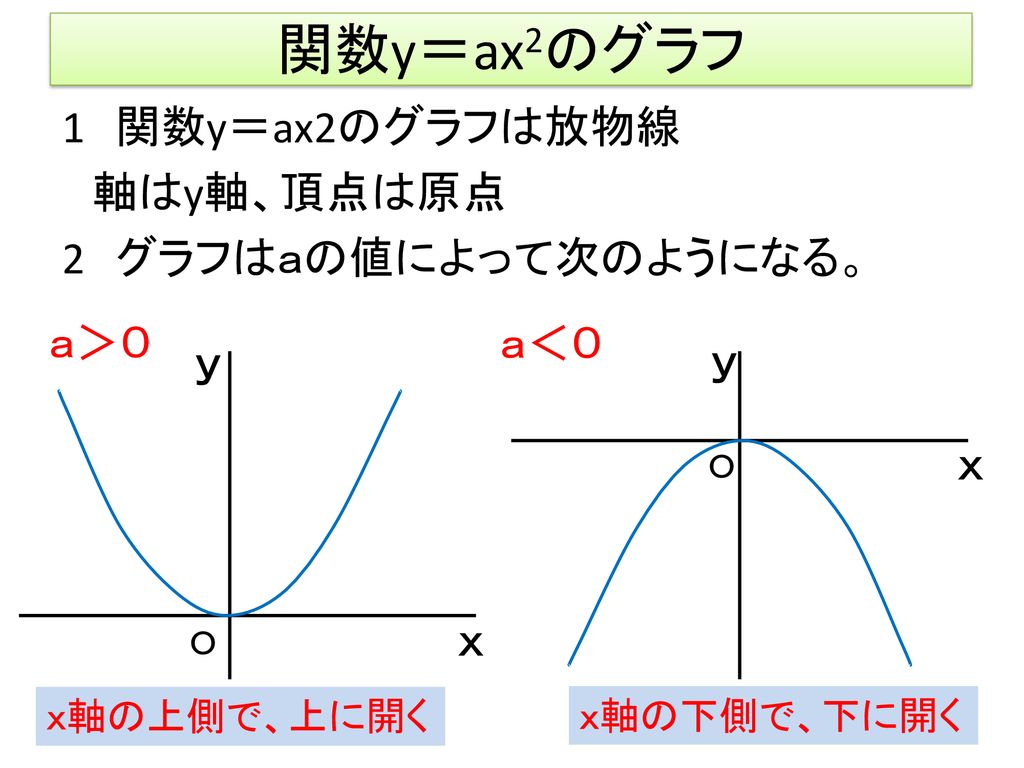
②変化の様子、グラフの形、 y=ax2のaの意味、変化の割合の意味など、関数y=ax2の特徴を理解している。 関数y=ax2の利用 ③関数y=ax2の関係が実生活に深くかかわっていることに気付き、関数y=ax2を活用しようとする。二次関数y=ax2の放物線の5つの特徴 ゆうき先生 y=ax2の放物線には5つの特徴があるよ。 曲線 上下逆さまの2パターン y軸で線対称 定数aが正負の<関数y=ax2 のグラフの特徴> <グラフの開き> ・線対称、線対称、x軸の上側にあるということ を記載 y=2x2 のグラフとy=x2 のグラフを比べる →y=1 2 x2 のグラフ →y=ax2 で、a<0のときのグラフ(y=-x2 のグラフ) ・y=-x2 のグラフ → y=-2x2、y=- 1 2 x2 のグラフ → y=ax2 のグラフ
A,Bの座標が次のそれぞれの場合において、y=ax 2 のグラフが線分AB(両端を含む)と交わるようなaの値の範囲を求めよ。 A(2,1), B(2,8) A(4, 4), B(4, 8) A(3, 1), B(3, 9) 図の放物線lはy= 1 2 x 2 の グラフで、放物線mはy=ax 2 のグラフである。lとmがx軸に平行な直線nと交わる点をそれぞれA, Bとする。Aのx座標が・関数y=ax2として捉えられる二つの数量について,変化や対応の特徴を見いだし,表,式,グラフを相互 に関連付けて考察し表現すること。 ・関数y=ax2を用いて具体的な事象を捉え考察し表現すること。 <単元指導計画(ねらいと評価 規準 )>・関数y=ax2のグラフとaの値の関係 関数 y=ax2のグラフとその特徴を理解 し,グラフをかくことができる。 8 9 ・グラフから,関数y=ax2のyの増減を 調べる。 ・xの変域からyの変域を求める。 グラフから,y=ax2関数のyの増減を調




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ




Y Ax 2 Cのグラフ 数学i フリー教材開発コミュニティ Ftext
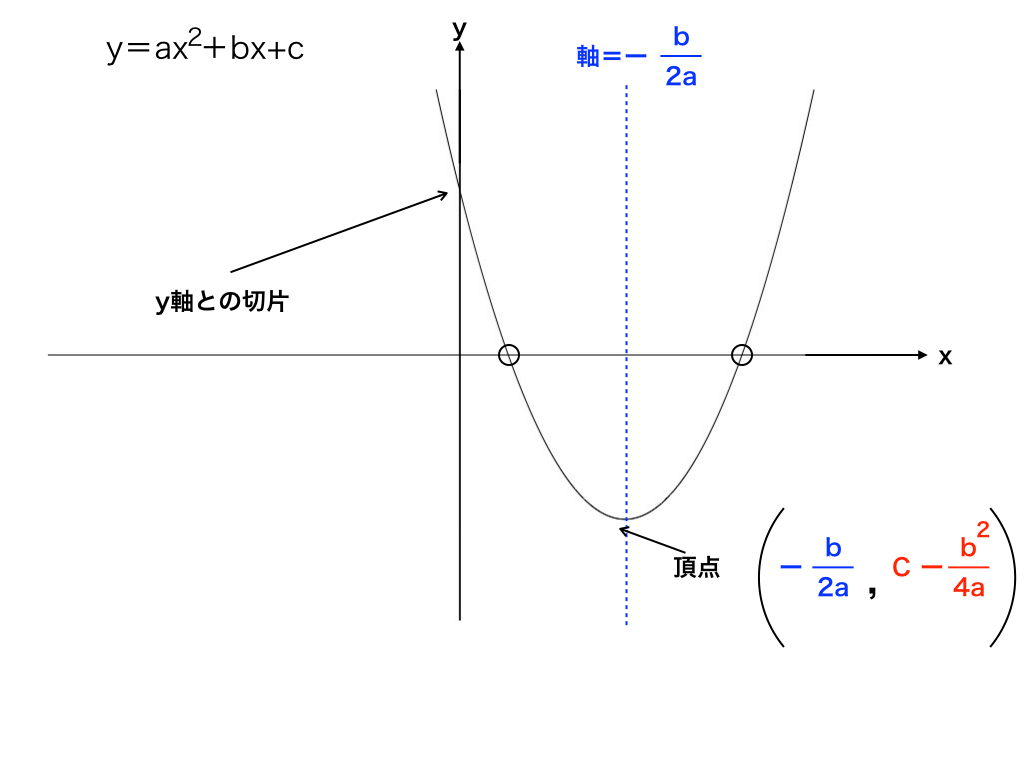
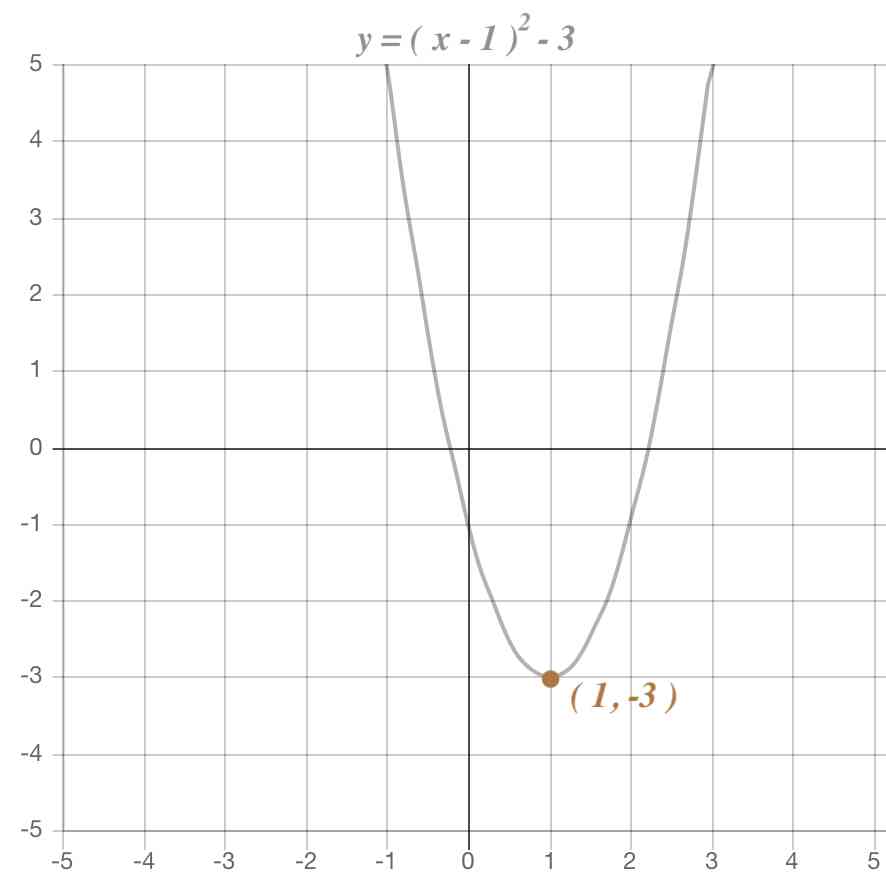
書誌 数学教育 05年11月号 著者 杉田 慶也 ジャンルの「変化の割合」? (2乗に比例する関数) 中3生の「数学」のコツ 2乗に比例する関数 ( y = ax²・関数y=ax2のグラフや 変化の割合などの特徴を 理解している。 ・具体的な事象の中で,関数 y=ax2の用い方を理解グラフの頂点は、y=ax²bxcを平方完成してy=a(x−p)²+qの形にすることで求めることができましたね。



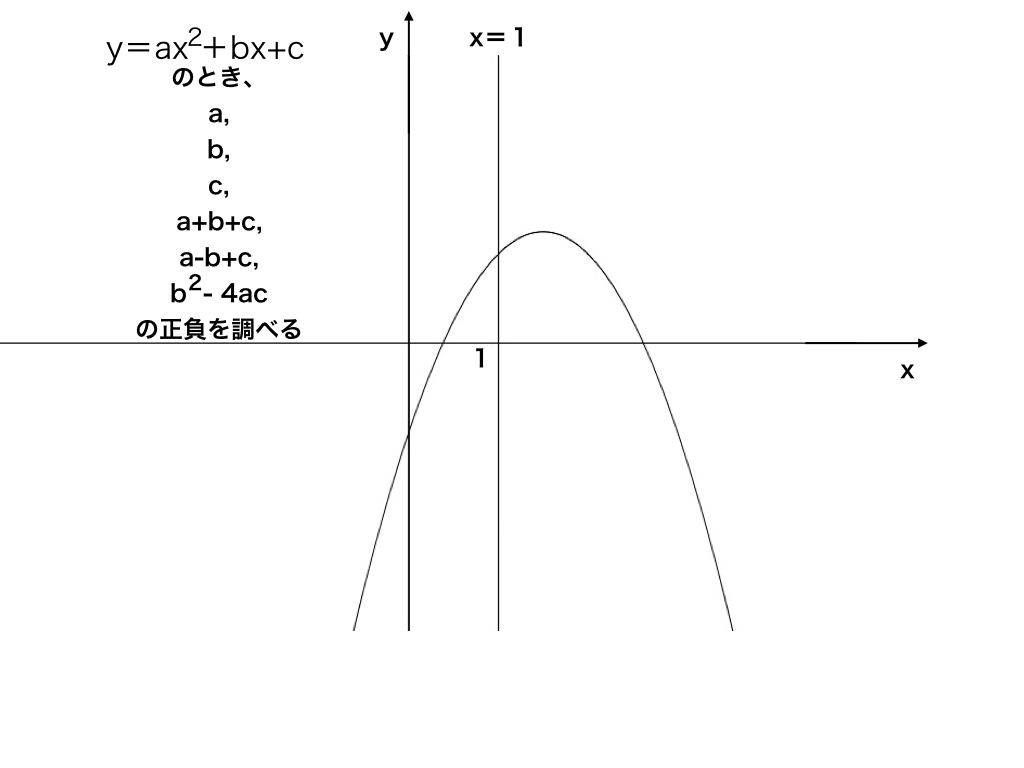
二次関数のグラフと解の存在範囲の問題をわかりやすく解説




中3 Y Ax二乗のグラフの性質 変域の求め方 中学生 数学のノート Clear
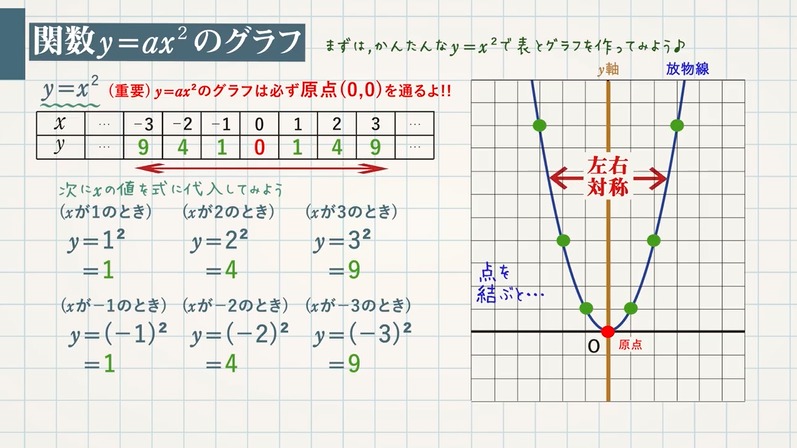
このページでは、二次関数のグラフを決定するのに必要な要素や、グラフの特徴について解説します。 グラフの形と位置 について説明することだと思います。 では、グラフの形や位置と、 y = a x 2 b x c という式はどんな関係になっているのでしょうか1節 関数とグラフ 表をつくり、対応や変化を調べることを通して、y=ax2で表される関数があることとその特徴を理解すること 関数y=ax2でyはxの2乗に比例するという見方をすること 与えられた条件からy=ax2の式を求めること 1 関数y=ax2 2 関数y=ax2のグラフ2 2 乗に比例する関数のグラフ ここでは,関数y=ax2 のグラフとその特徴について学習してみましょう。 関数y=ax2 において,x=k,-kのときのyの値をそれぞれ求 めると,ともに



二次関数のグラフの書き方



中学生がつまずきやすい数学分野
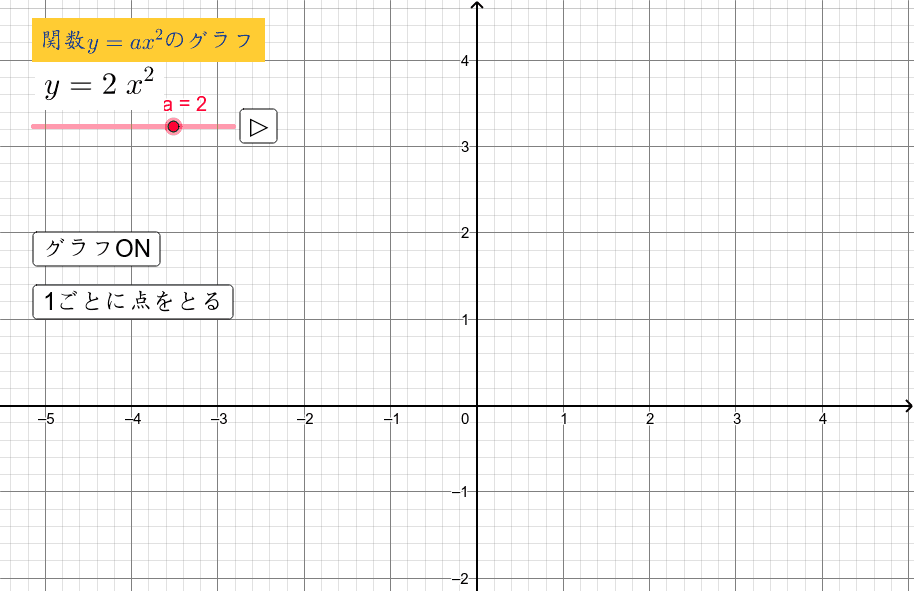
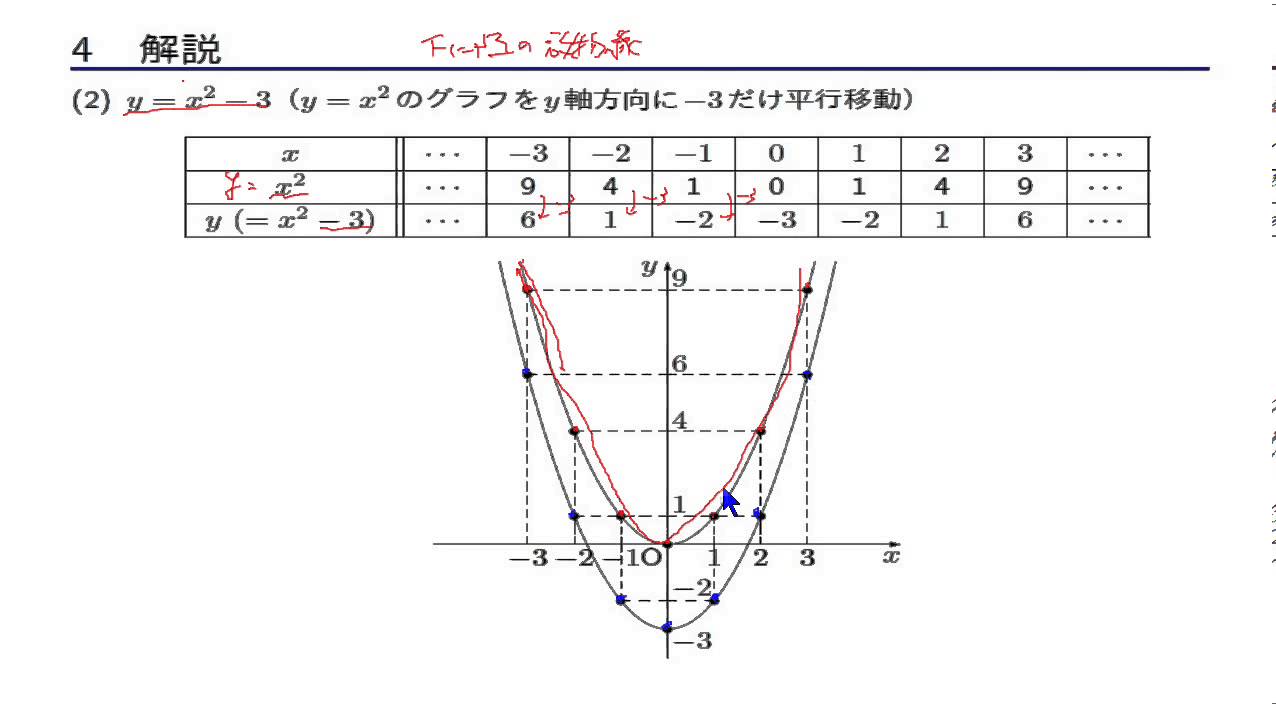
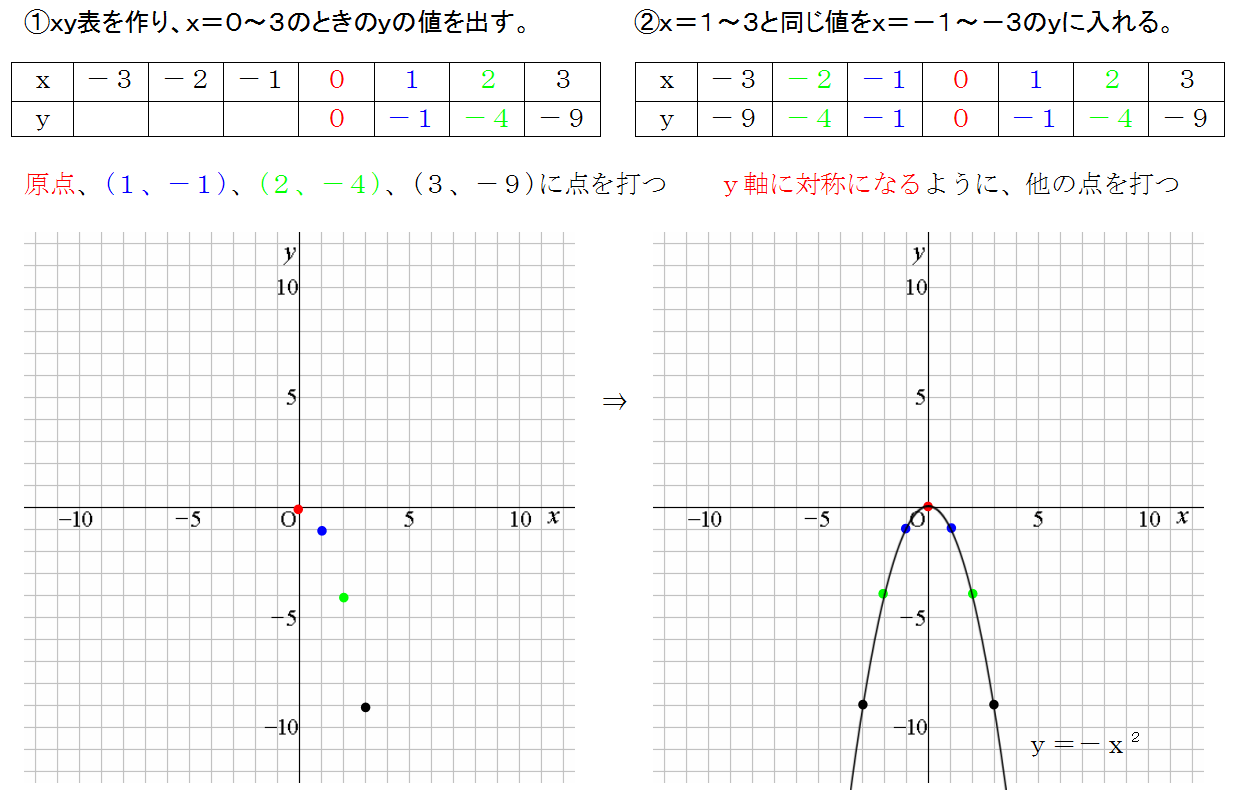
・学習活動:2次関数y = ax2 q の軸、頂点、グラフ ・指導上の留意点:2次関数 y = ax2 とy = ax2 q のグラフをかき、平行移動及びグラフの特徴を理解させる。2次関数 y = ax2 qの軸の方程式、頂点の座標を求めさせる。 ・評価(観点、方法等):y =2乗に比例する関数のグラフは直線ではないため、 できるだけたくさんの点をとりフリーハンドでなめらかな曲線のグラフをかく。 y= 1 4 x 2 のグラフの書き方 xの値を式に代入して下の表を埋める。 → x 8 6 4 2 0式,グラフを関連 式,グラフを用いて,を相互に関連付けるで表現したり,表,変化の割合など,関 ( 付けて理解する。本その特徴を調べようなどして見いだすこ式,グラフから,そ数y=ax2 の特徴を理 時としている。 とができる。




中3数学 Y Ax 2のグラフ A 0 映像授業のtry It トライイット



二次関数のグラフの書き方
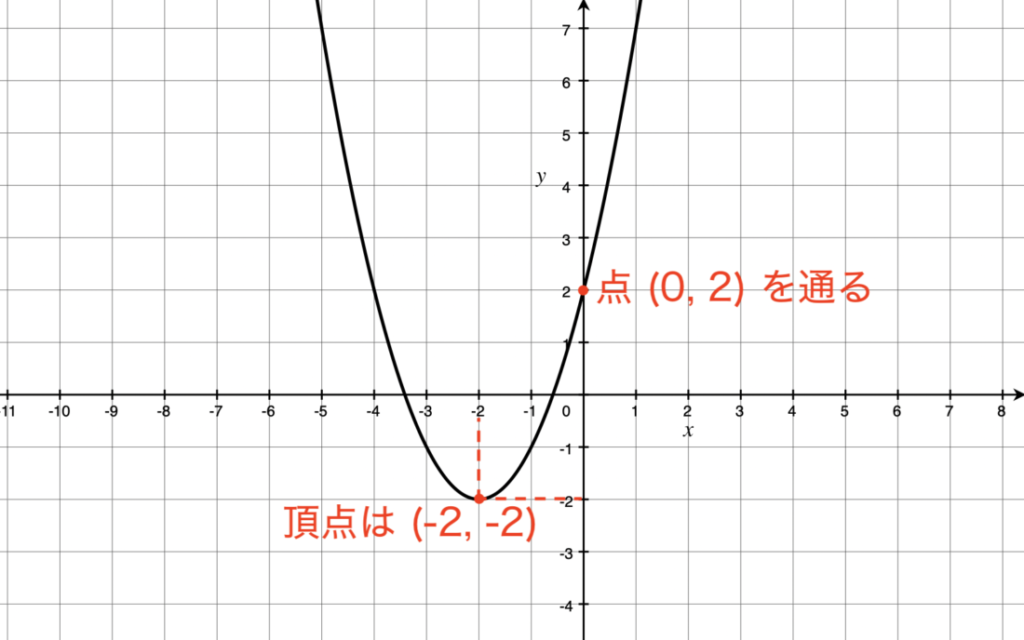
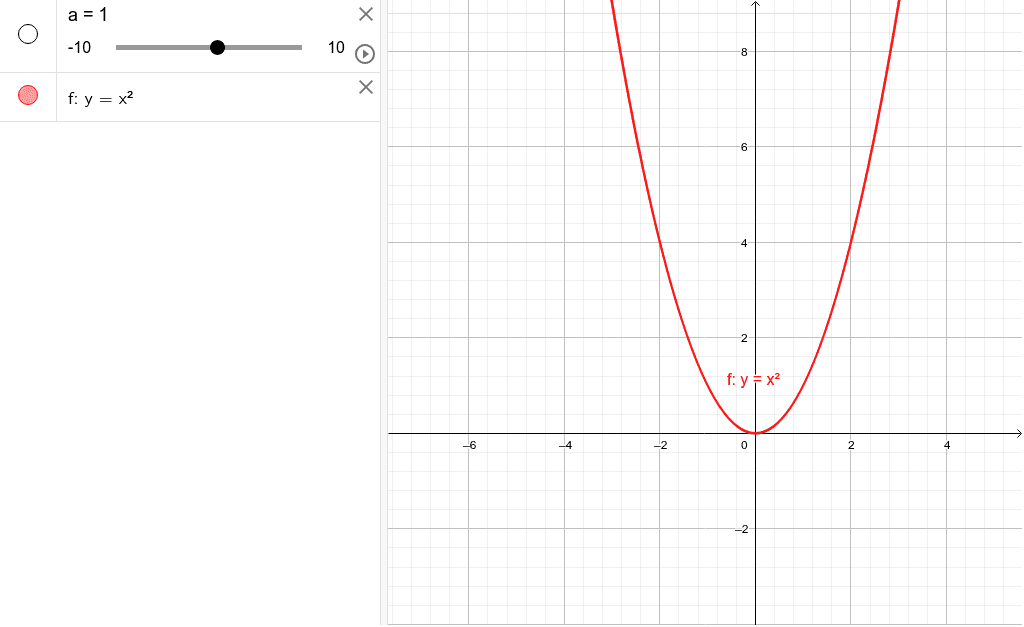
2次関数のグラフは,放物線とも呼ばれ,ボールを遠投したとき描く曲線のような形をしています。 その曲線を式で書くと,y=ax2 (a≠0) の形に書かれます。 この章では,この曲線について,前の章で学んだ平行移動を行なうことにします。 まず,y=ax2 の性質と,これから使う名称について説明しておきます。 a は 0 以外の適当な数ですが,この値によって,グラフの二次関数 y=ax^2 のグラフ 二次関数 y = ax2 bx c y = a x 2 b x c について調べるためには、このグラフがかけた方がいいのですが、どうやってかけばいいのでしょうか。 まずは、 y = ax2 y = a x 2 の場合について、考えていくことにしましょう。 とてもシンプルY=ax2乗のグラフで覚えておきたい用語 まず、グラフの形は 放物線 となります。 この放物線は左右対称の形となっており、その折れ目となる線のこと




例題で学ぶ高校数学 Y Ax2 Q




例題で学ぶ高校数学 Y Ax2
印刷用紙:B4縦 1ページの行数:55 1行の文字数(半角で):114 中 学 校 数 学 科 (3 年) 指 導 プ ロ グ ラ ム 学校名 大槌町) の「変化の割合」とは? 中3生の「数学」のコツ 中学生から、こんなご質問をいただきました。 「2乗に比例する関数(y=ax²)で、 "変化の割合"は、 "a の値"とは違うものなのですか? 」Y=ax2 の問題 y=ax2 のグラフ y=ax2 のグラフの特徴 y=ax2 の値の増減と変域 変域 変化の割合 10月 年間プラン7 2乗に比例する関数2 いろいろな関数




2次関数 Y Ax Qのグラフの書き方 グラフの平行移動 数学i By ふぇるまー マナペディア



二次関数のグラフと解の存在範囲の問題をわかりやすく解説
№15発展関数y=ax2 ② 組 氏名 問1次の関数のグラフをかきなさい。 ①=3 ②yx y x2 2=-2 ③= ④yx y x2 2=- 1 3 2 3 y x O 555 5 15 問2次の図で,①~④の4つの関数のグラフは,授業を通して,生徒は,導入段階で既に関数y=ax 2 の表,式,グラフの特徴の一部を捉えることができていた。以後の授業では,生徒自らが捉えた関数y=ax 2 の表,式,グラフの特徴を基に授業を進めることができた。結果,生徒は課題意識をもって授業に取り組み,知識・技能の定着の度合いも良好で4 ・関数y=aχ2 のグラフ のかき方とその特徴を理解 する。 ・関数y=aχ2 のグラフをかくことができる。 ・関数のグラフの特徴を、比例定数の符号や絶対値 と関連付けて理解している。 (行動・発言・ノート・ワークシート)



二次関数y Ax2の放物線にみられる5つの特徴 Qikeru 学びを楽しくわかりやすく
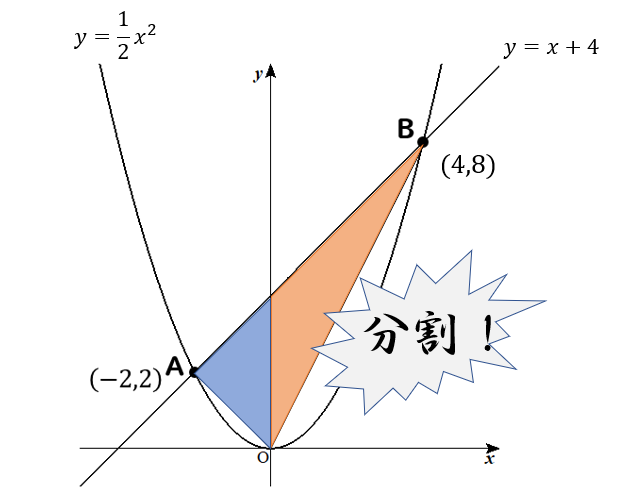



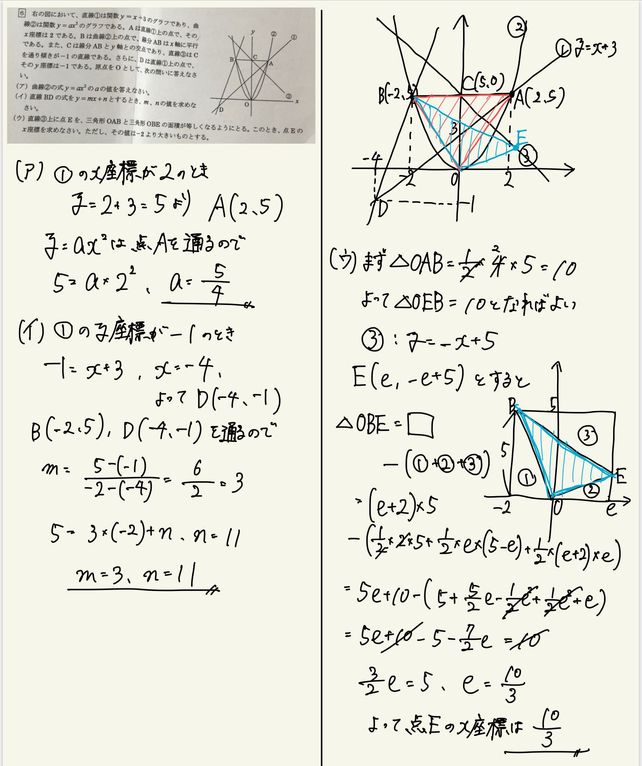
Y Ax2乗の利用 放物線と直線による面積 中学3年の問題をイチから解説 中学数学 理科の学習まとめサイト
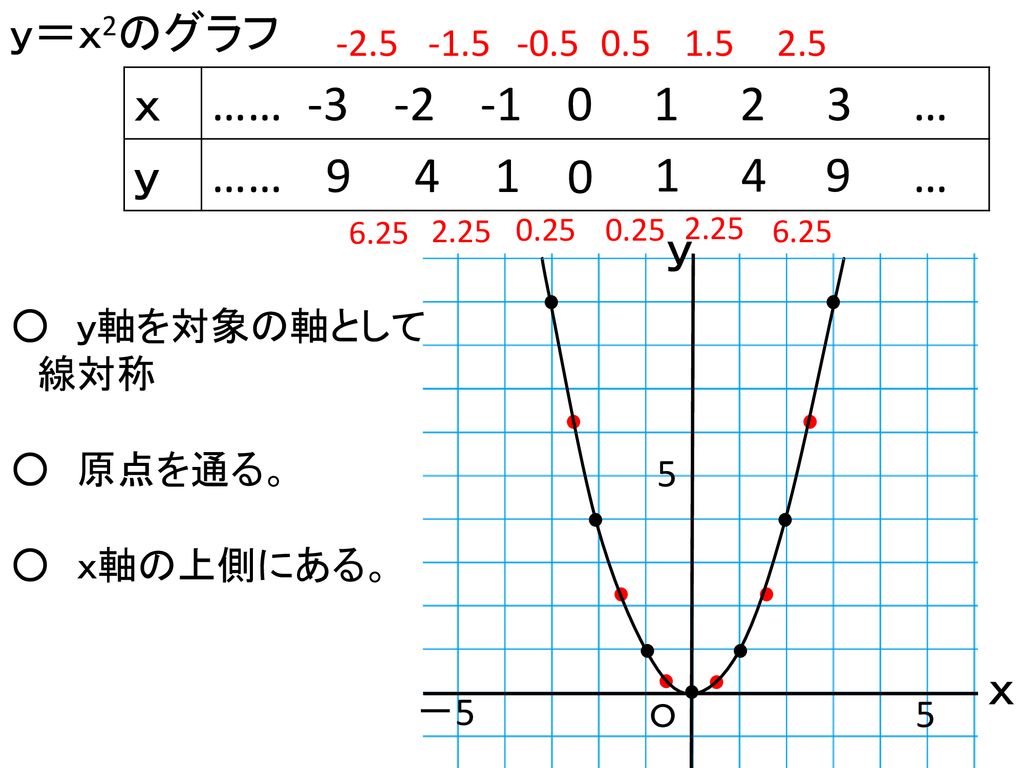
・関数y=ax2のグラフの特徴をまとめる。 2乗に⽐例する関数の値と変化 ・関数y=ax2の値の増減について調べる。 ・関数y=ax2で,xの変域に対応するyの変域を求める。 2乗に⽐例する関数の利⽤ ・⾝のまわりの問題を,関数y=ax2のグラフを利⽤して解決 する。Y = ax2 y = a x 2 2乗に比例 y y が x x の関数であり、 x x と y y の間に y = ax2 y = a x 2 という関係式が成り立つとき、 y y は x x の 2 2 乗に比例する という。 ただし、 a a は 0 0 でない定数で、比例定数といいます。 「 y y は x x の 2 2 乗に比例する」と問題文に重要 関数y=ax2 のグラフは放物線とよばれる曲線である。放物線の対 称の軸(対称軸)を放物線の軸といい,軸との交点を放物線の頂点と いう。 関数 y=ax2 のグラフの特徴 ・原点を頂点とする放物線で,y軸について対称になっている。




二次関数y Ax2の放物線にみられる5つの特徴 Qikeru 学びを楽しくわかりやすく



中学数学 関数
② 関数y=ax2について,表,式,グラフを相互に関連付けて理解することができる。 ③ 関数y=ax2を用いて具体的な事象をとらえ説明することができる。 ④ いろいろな事象の中に,関数関係があることを理解することができる。 〈重点目標〉Y=ax2 グラフ Y Ax のグラフ 中学3年 数学クラブ 中学数学 1次関数と2次関数y Ax2のグラフの3つの違い Qikeru 学びを楽しくわかりやすく与えられた条件からy=ax2の式を求めること 2 関数y=ax2のグラフ C(1)イ 関数y=ax2のグラフとその特徴 関数y=ax2のグラフとaの値との関係 ☆方眼のないグラフで,y=ax2のaの値の違いから式とグラフの対応を判断し,説明する活動を通して関数y=ax2のグラフ




数学 中3 35 二次関数のグラフ Youtube



数学の問題です 図のように関数y Ax2 2乗 のグラフ上に3点a B Yahoo 知恵袋
式、値の変化、グラフなどから関数関係を分析し、その特徴を理解し、問題を関数的に解決する y = ax2 y = a x 2 の関係にある数量を、表、式で表したり、変数の変域、変化の割合を求めたり、曲線上の2点を通る直線の式を求めることができる 関数 y = ax2 y = a x 2 ・変化の割合の意味,関数 y = ax2 y = a x 2 のグラフの特徴,直線の式の求め方を理解する・関数y=ax2のグラフや 変化の割合などの特徴を 理解している。 ・具体的な事象の中で,関数 y=ax2の用い方を理解閲覧ありがとうございます。 関数y=ax2のグラフについてです。 y=1/2x2についてグラフをかくのにまず私は比例の表?みつけたグラフの特徴は性 質と結びつけて演繹的に言 い切れるかな? これまで学習した関数は どのような日常場面にあ らわれるの? 与えられた情報で式を求めら れる方法は,これまでの関数 の学習と同じ? 2次関数の一般式y=ax2bxc はどんな関数かな?
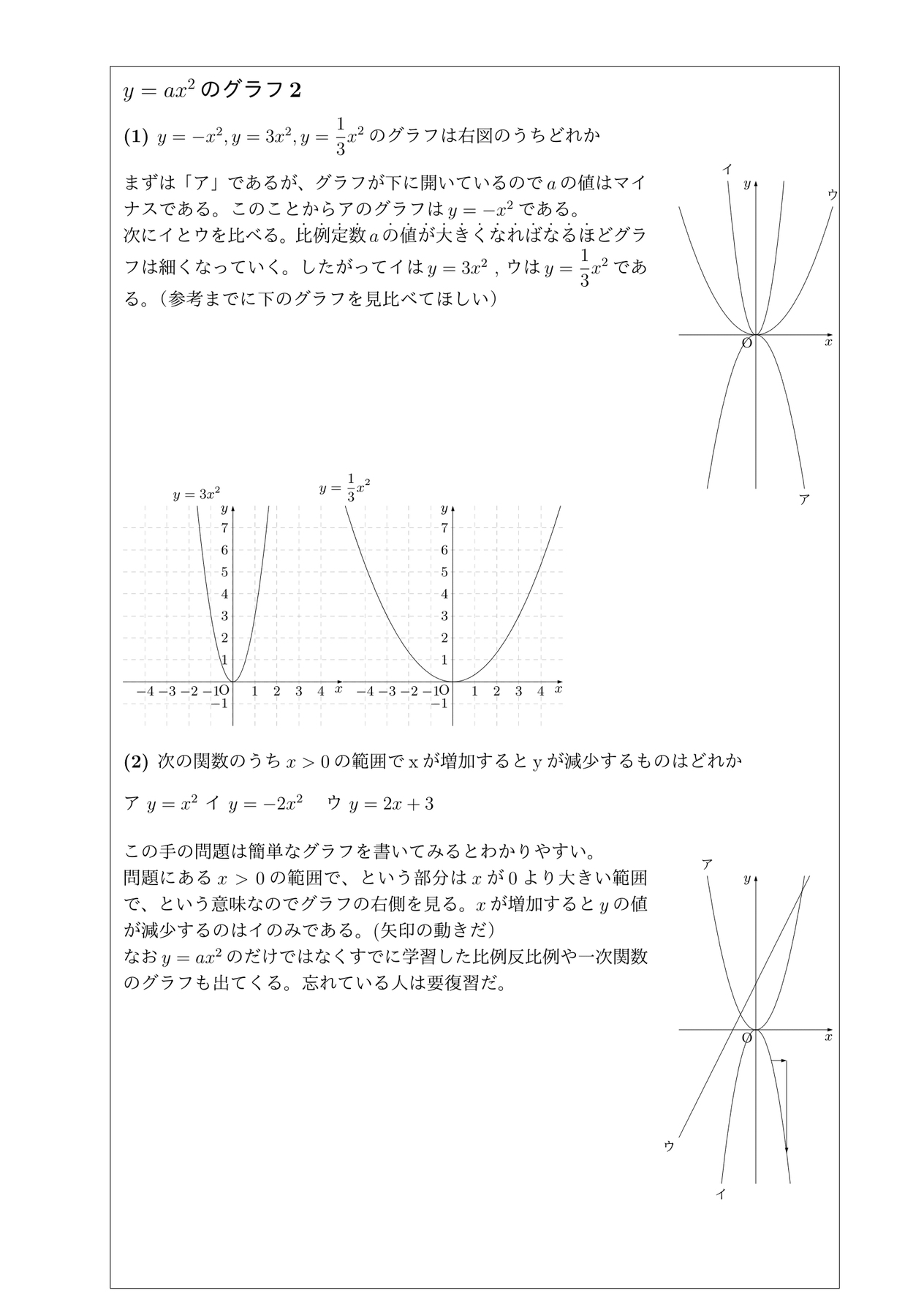



Y Ax 2のグラフの特徴 チーム エン



二次関数のグラフの書き方



4 関数 Y Ax 2 1章 関数とグラフ 3 関数 Y Ax 2 の値の変化 5時間 Ppt Download



関数y Ax2乗の変域の求め方 勉強ナビゲーター




二次関数のグラフの問題 aの値で上か下かの向きが決まるよ 中学や高校の数学の計算問題



関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ



2次関数とは 1分でわかる意味 公式と計算 グラフ 平行移動との関係
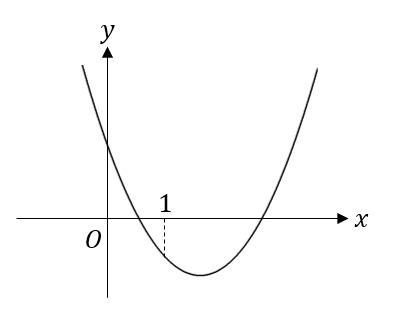



二次関数 係数の符号の決定 グラフから符号を決めるポイントを解説 数スタ
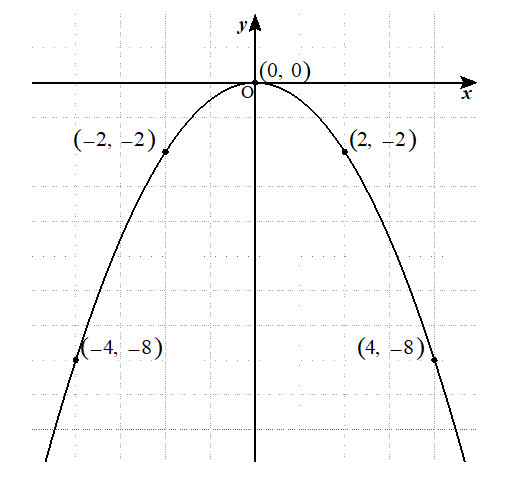



関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ




関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ




高校数学 Y Ax 2 Bx Cのグラフ 例題編 映像授業のtry It トライイット



Www Pref Tottori Lg Jp Secure Tyusuu Pdf




高校数学 Y Ax 2のグラフ 下に凸 上に凸 映像授業のtry It トライイット




Y Ax2乗の利用 放物線と直線による面積 中学3年の問題をイチから解説 中学数学 理科の学習まとめサイト



1




Y Ax2乗 グラフの特徴と書き方をイチから解説します 中学数学 理科の学習まとめサイト




Y Ax2乗 変域の求め方 変域から式を作る方法について解説 中学数学 理科の学習まとめサイト




中学数学 二次関数y Ax2のグラフの書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




Y Ax 2 Bx Cのグラフ 数学i フリー教材開発コミュニティ Ftext




中学数学 二次関数y Ax2のグラフから式を3秒で読み取る方法 Qikeru 学びを楽しくわかりやすく
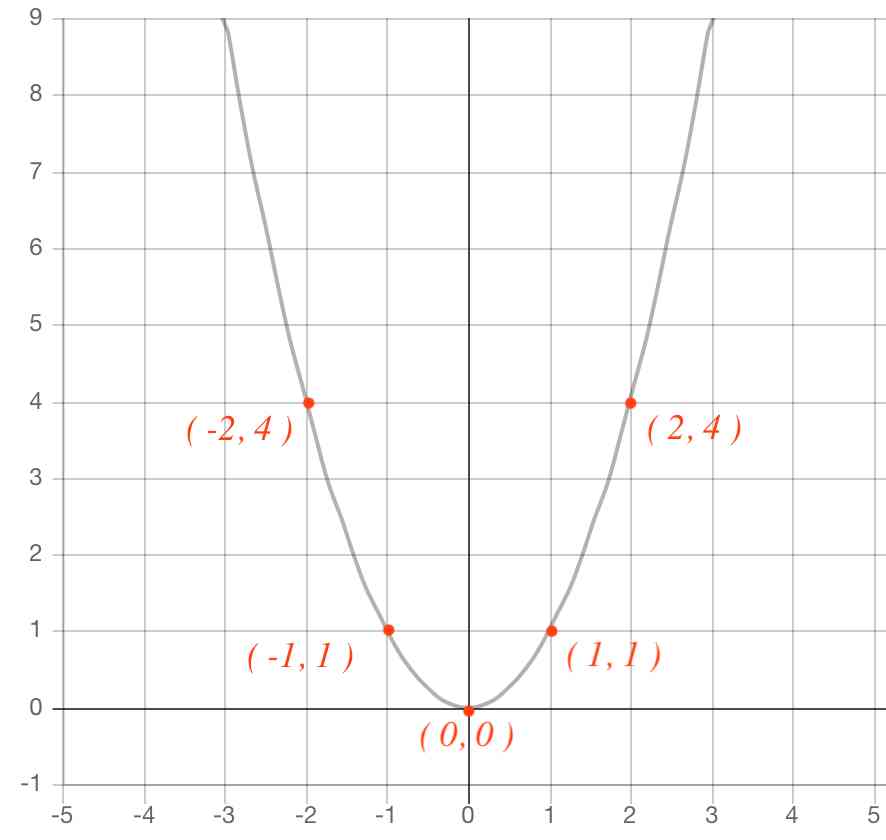



二次関数のグラフの書き方
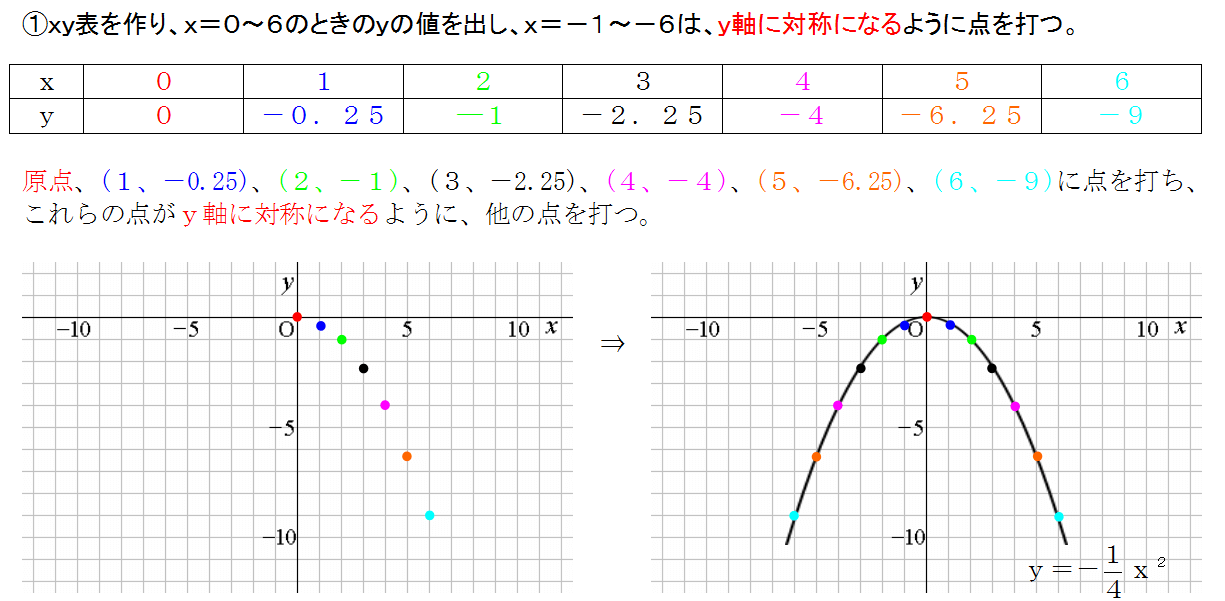



二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師




中学数学 二次関数y Ax2のグラフから式を3秒で読み取る方法 Qikeru 学びを楽しくわかりやすく




Yax2 Y Descubre Como Resolverlo En Qanda




高校数学 Y Ax 2 Bx Cのグラフ 練習編 映像授業のtry It トライイット




二次関数のグラフの書き方とグラフの問題を一気に紹介 スタディクラブ情報局




関数y Ax2乗 変域の求め方 変域から式を求める問題を解説 Youtube




Y Ax2乗 Aの求め方についてパターン別に解説 発展問題もアリ 中学数学 理科の学習まとめサイト
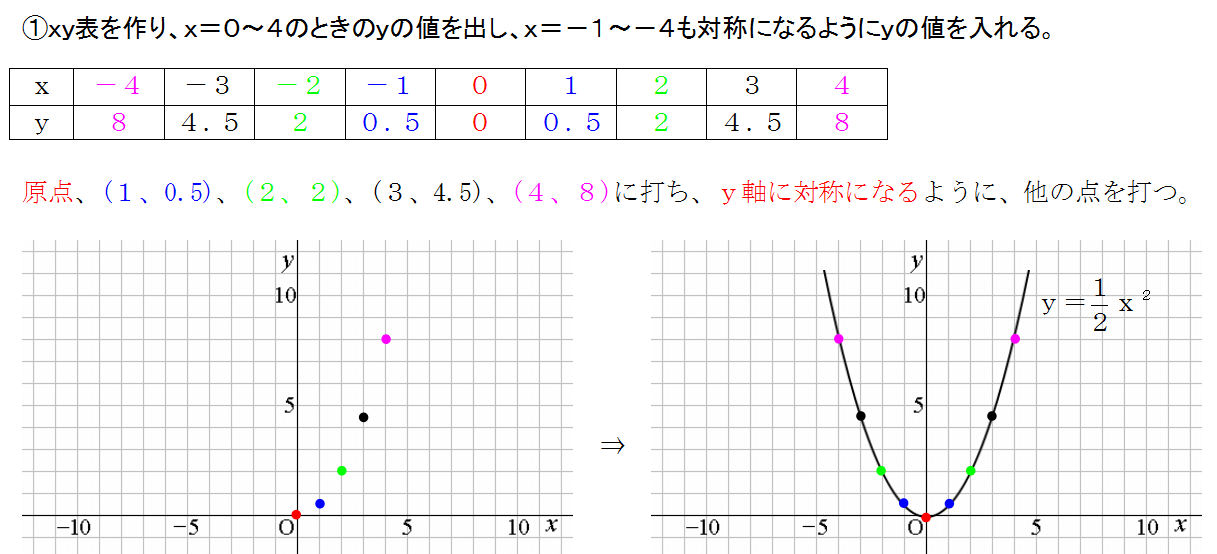



二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師



関数の変域 まなびの学園
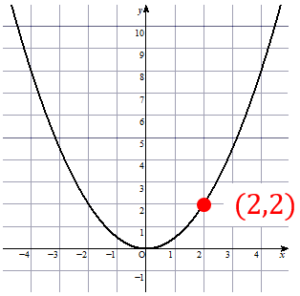



Y Ax2乗 グラフの特徴と書き方をイチから解説します 中学数学 理科の学習まとめサイト



Yax2 Descubre Como Resolverlo En Qanda



1
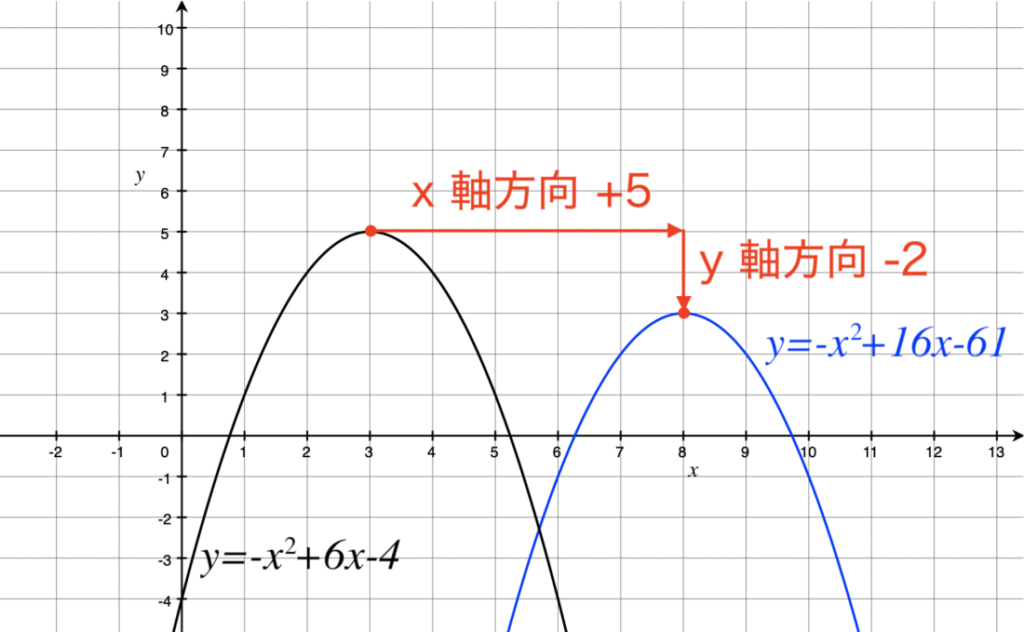



二次関数のグラフの書き方とグラフの問題を一気に紹介 スタディクラブ情報局



1



Y Ax のグラフ 中学3年 数学クラブ



Y Ax 2



二次関数のグラフの書き方とグラフの問題を一気に紹介 スタディクラブ情報局



関数y Ax2乗 放物線グラフの書き方はこれでバッチリ Youtube



中学生がつまずきやすい数学分野



関数y Ax 2のグラフ Geogebra



数学i 2次関数 2 2 Y Ax 2 Qのグラフ Youtube
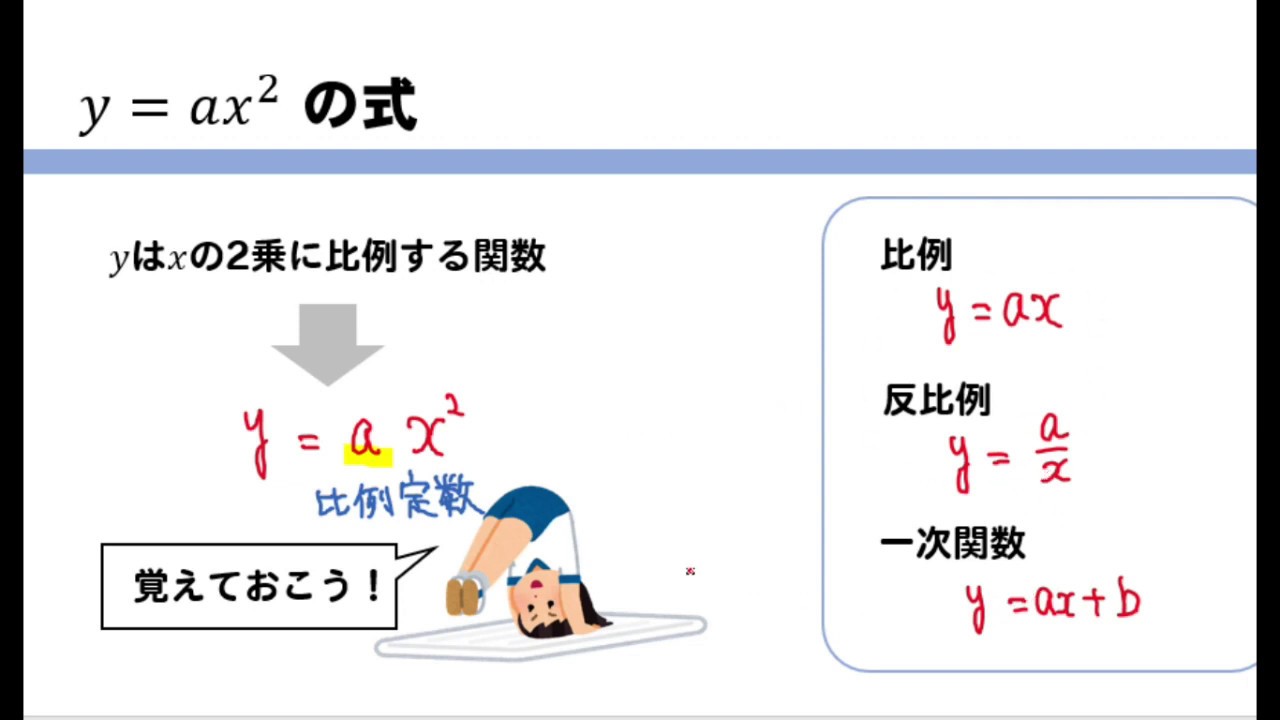



関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは Youtube
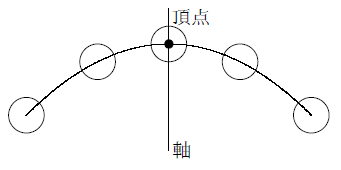



関数y Ax2のグラフ まなびの学園




関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ




基本 二次関数 Y Ax 2 のグラフ なかけんの数学ノート
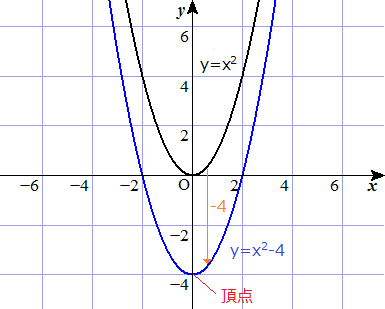



例題で学ぶ高校数学 Y Ax2 Q
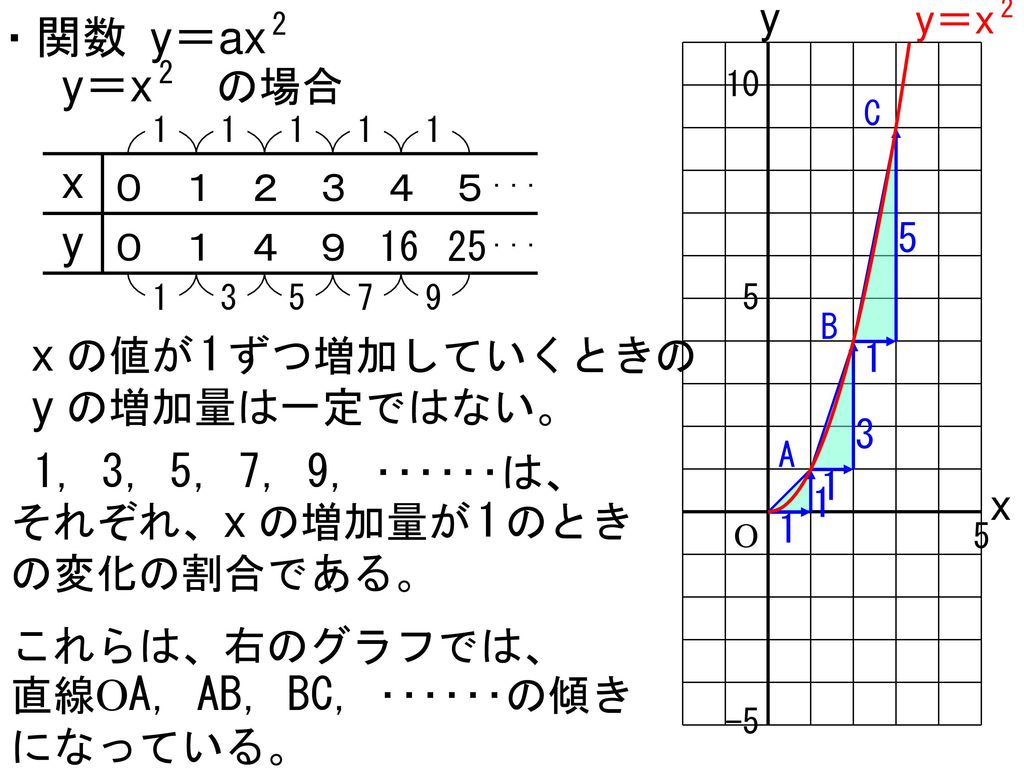



4 関数 Y Ax 2 1章 関数とグラフ 3 関数 Y Ax 2 の値の変化 5時間 Ppt Download



ねらい 関数y ax2のグラフをかき その特徴を理解する Ppt Download




2次関数のグラフ



Y Ax 2のグラフ Geogebra




例題で学ぶ高校数学 Y Ax2




二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ




基本 二次関数 Y Ax 2 のグラフ なかけんの数学ノート




基本 二次関数 Y Ax 2 のグラフ なかけんの数学ノート




2次関数のグラフと直線



二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師



ねらい 関数y ax2のグラフをかき その特徴を理解する Ppt Download




中3数学 2次関数のグラフの特徴と練習問題




y が x の2乗に比例する関数のグラフ 算数 数学が好きになりmath




関数y Ax2乗のグラフの書き方を教えてください ཀ Clear
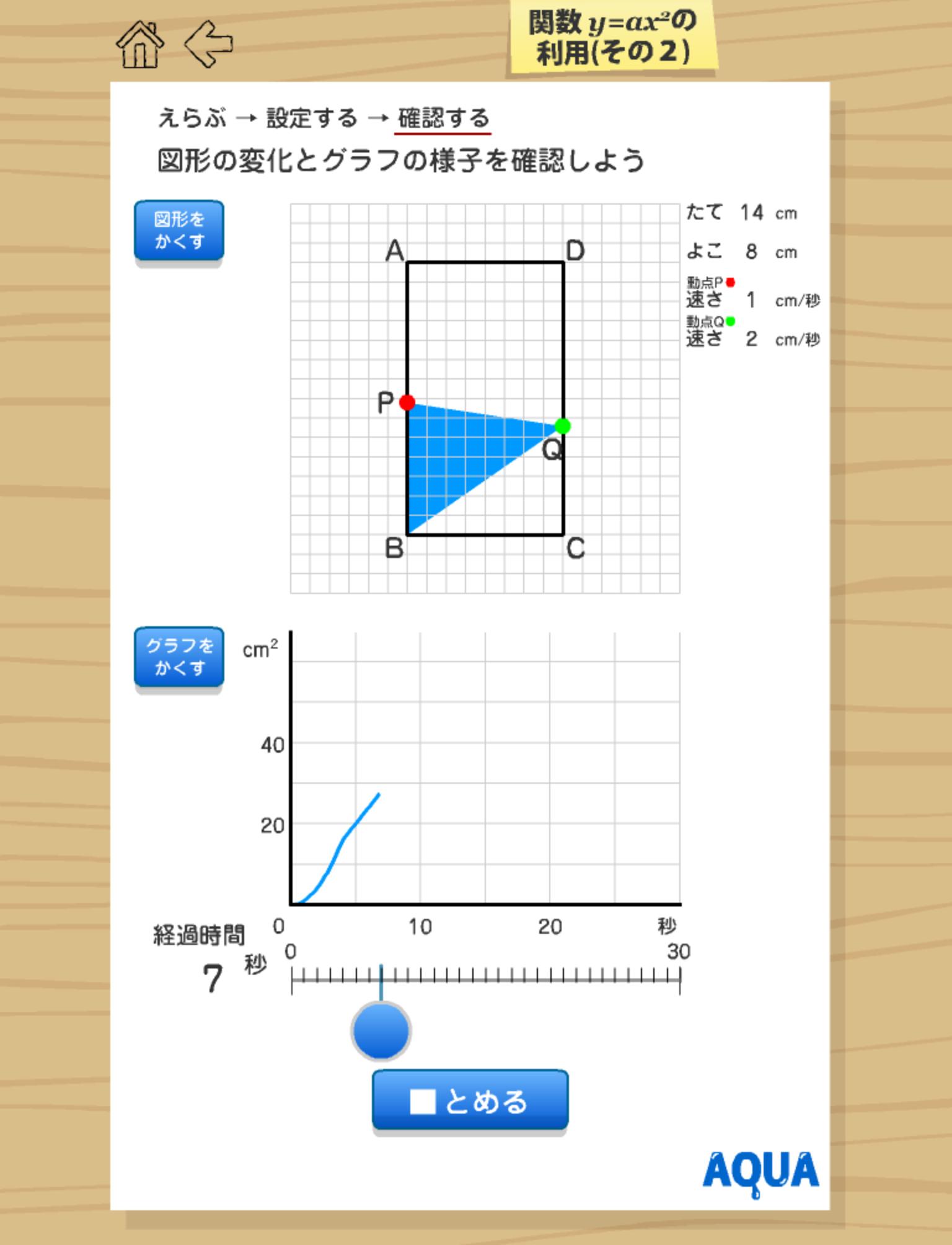



関数y Ax2の利用2 さわってうごく数学 Aquaアクア For Android Apk Download



2次関数とは 1分でわかる意味 公式と計算 グラフ 平行移動との関係




二次関数 Wikipedia




中3 関数 Y Ax2 まとめ 中学生 数学のノート Clear
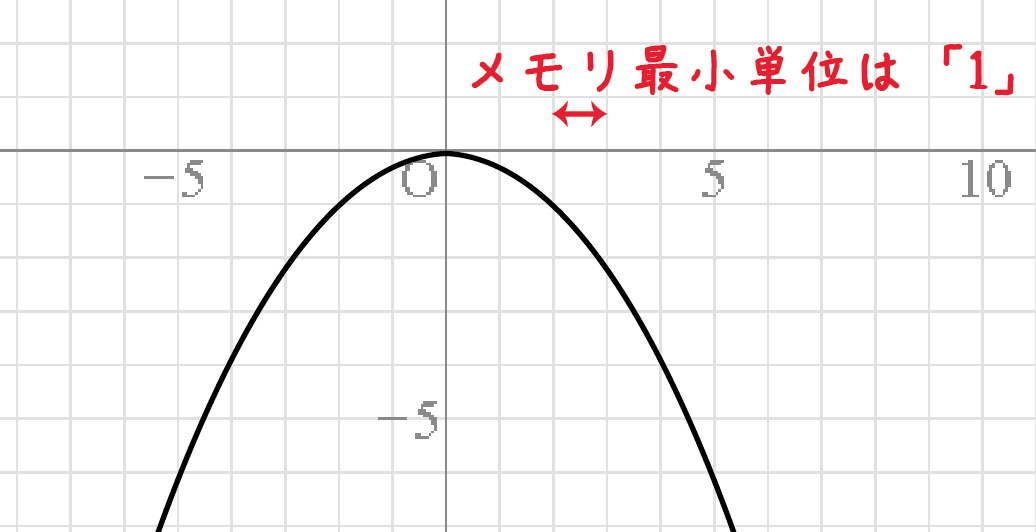



中学数学 二次関数y Ax2のグラフから式を3秒で読み取る方法 Qikeru 学びを楽しくわかりやすく



1
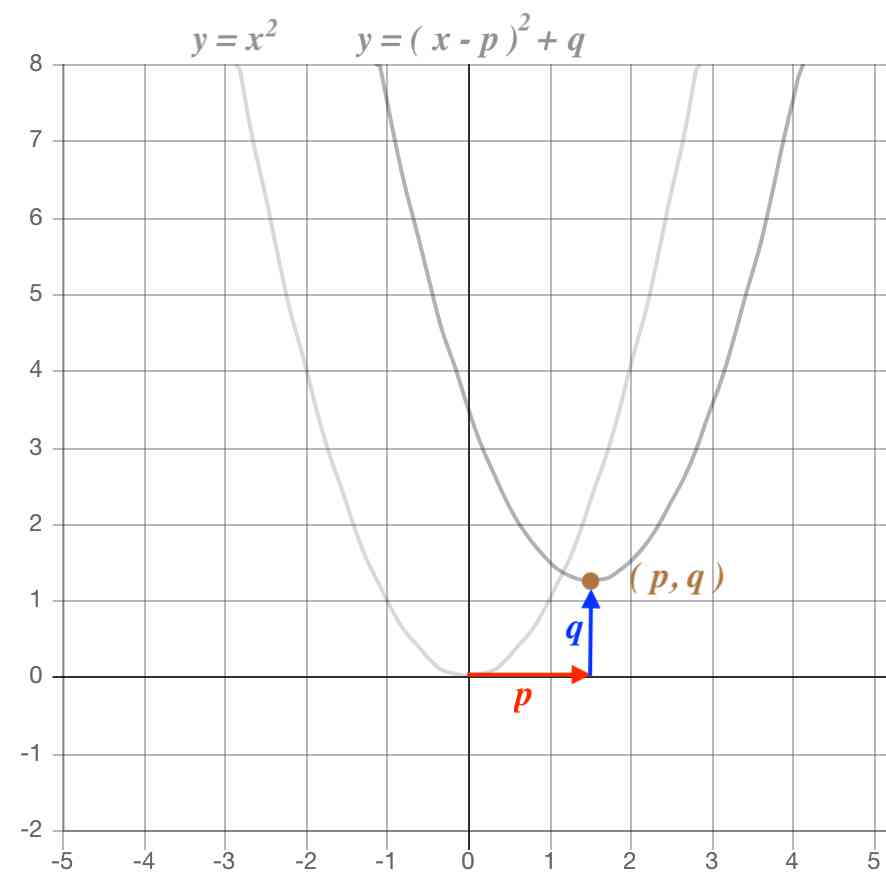



二次関数のグラフの書き方
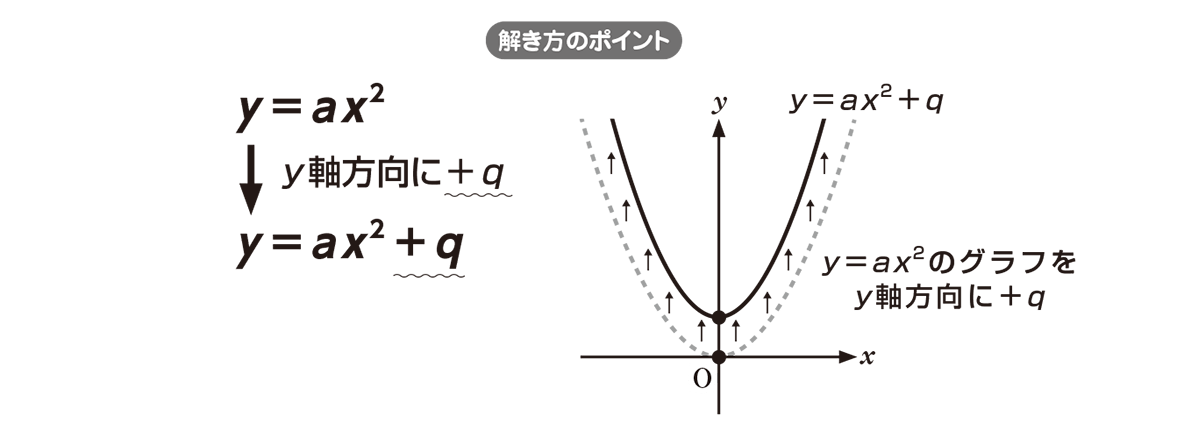



高校数学 Y Ax 2 Qのグラフ2 映像授業のtry It トライイット
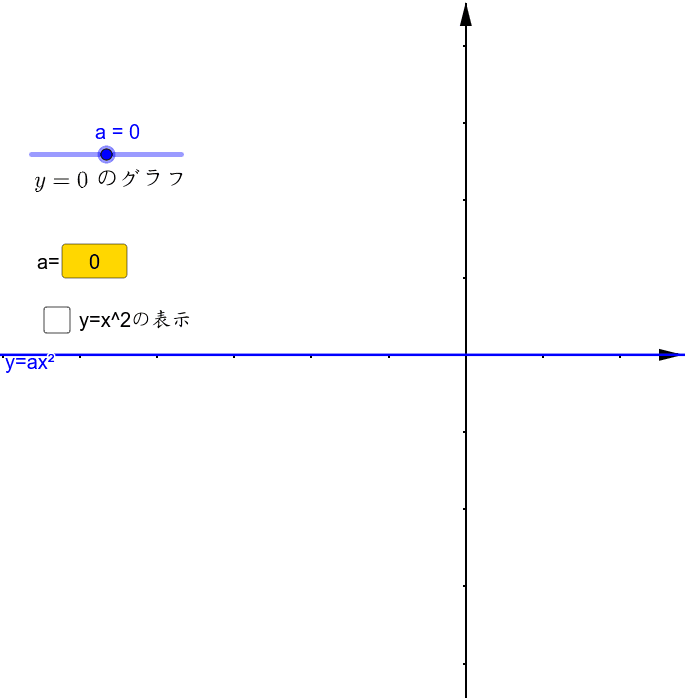



関数y Ax 2 Aの値によるグラフの特徴 Geogebra
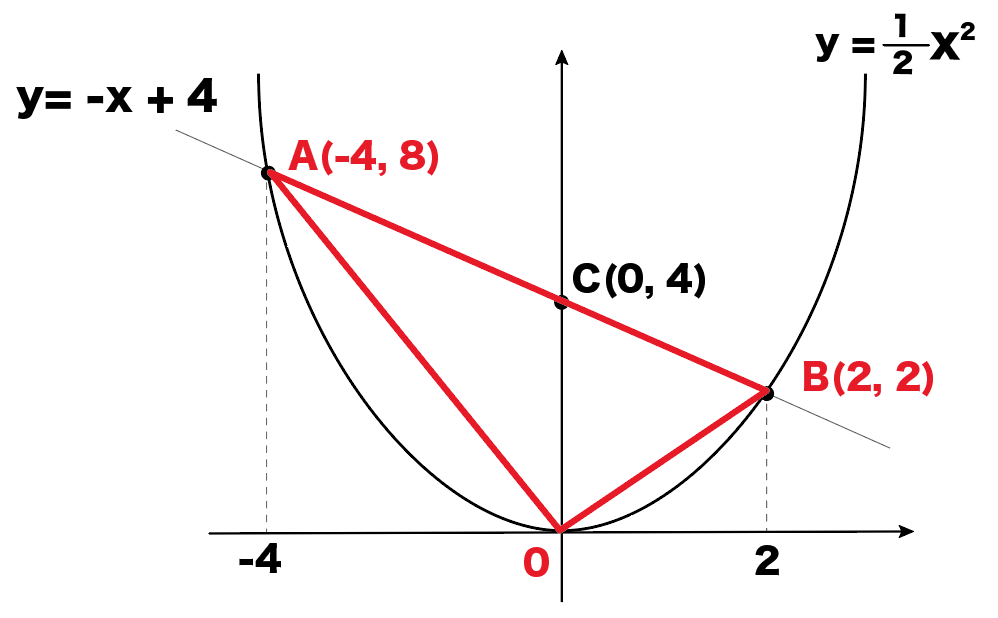



二次関数のグラフで三角形の面積を求める問題の解き方4ステップ Qikeru 学びを楽しくわかりやすく



二次関数のグラフの書き方と 頂点 軸 切片の求め方 受験辞典




関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ



Http Www Edu City Fukuyama Hiroshima Jp Chu Johoku Revolution Actionplan Syutaiteki Manabi01 6 Shidouan K29 07m Pdf



関数y Ax2のグラフ まなびの学園




2乗に比例する関数のグラフ 放物線 の書き方 無料で使える中学学習プリント
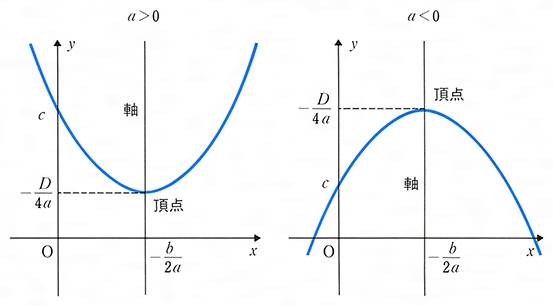



二次関数とは コトバンク
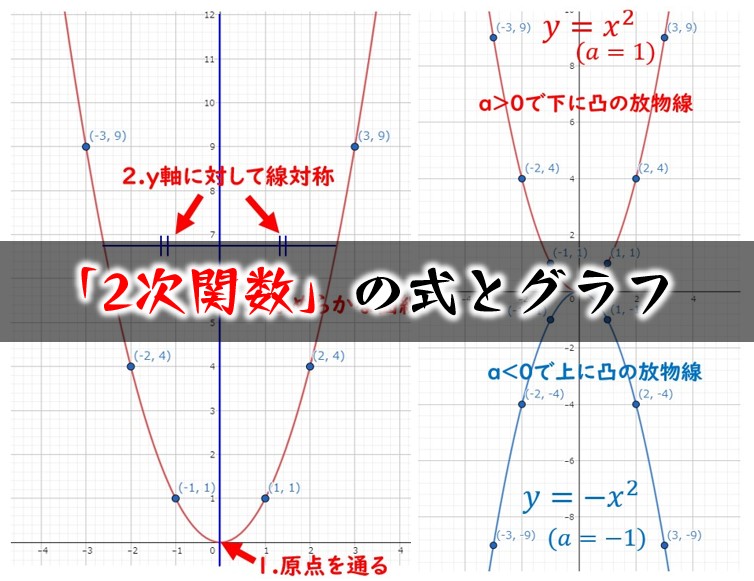



2次関数とは 式とグラフの解説 数学fun




二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ




Y Ax Bのグラフと 切片と傾きの意味 中学数学 By じょばんに マナペディア
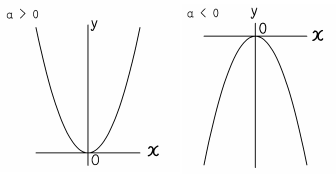



2乗に比例する関数 グラフ



Y Ax 2



関数y Ax2乗の変域の求め方 勉強ナビゲーター



関数y Ax のグラフの性質 教遊者



0 件のコメント:
コメントを投稿