円錐台の体積の求め方を覚えましょう ≪円錐台の体積の求め方≫ 図bのように円錐を作り、以下の式で答えを求めます。 (大きな円錐)-(小さい円錐)=円錐台 図b 図bを見ると、小さい円錐の高さ(〇㎝)と大きな円錐の高さ(〇+4㎝)を求めることが円錐の体積 円錐の体積は, V = 1 3πr2h V = 1 3 π r 2 h ( r r :半径, h h :高さ ) の公式で求めることができる. この公式は,円柱の体積の公式 V = πr2h V = π r 2 h に 1 3 1 3 をかけたものと考えることができるが,なぜ円柱の体積に 1 3 1 3 をかけることにより11月26日(火) 角錐の体積の求め方 6年生の算数の授業です。 角錐・円錐の体積の求め方には底面積×高さ÷3という公式があります。 「なぜ、÷3するのか」という疑問を解決するために、四角錐などの立体を組み合わせて考えました。 自分たちが体積を
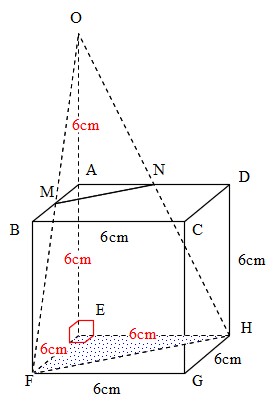
Mathematics 錐体の一部の体積 働きアリ
円錐台 体積 求め方
円錐台 体積 求め方- 円錐の体積を円柱座標系で真面目に計算してみた よく知られているように、円錐の体積は 1 3πR2h 1 3 π R 2 h です。 ここで底面の円の半径を R R 、高さを h h としました。 中学の数学などで天下り的に教わったのですが、導出は教わった記憶がありません円錐の体積を求める公式は、 V = 1/3 Sh = 1/3 πr^2 h で表されます。このページでは、例題と共に、円錐や円錐台の体積を計算する方法を説明しています。




M Sudo S Room 円錐台形の慣性モーメントに関する補足
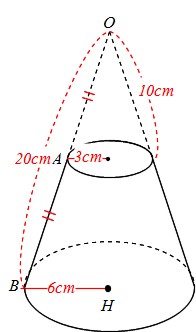
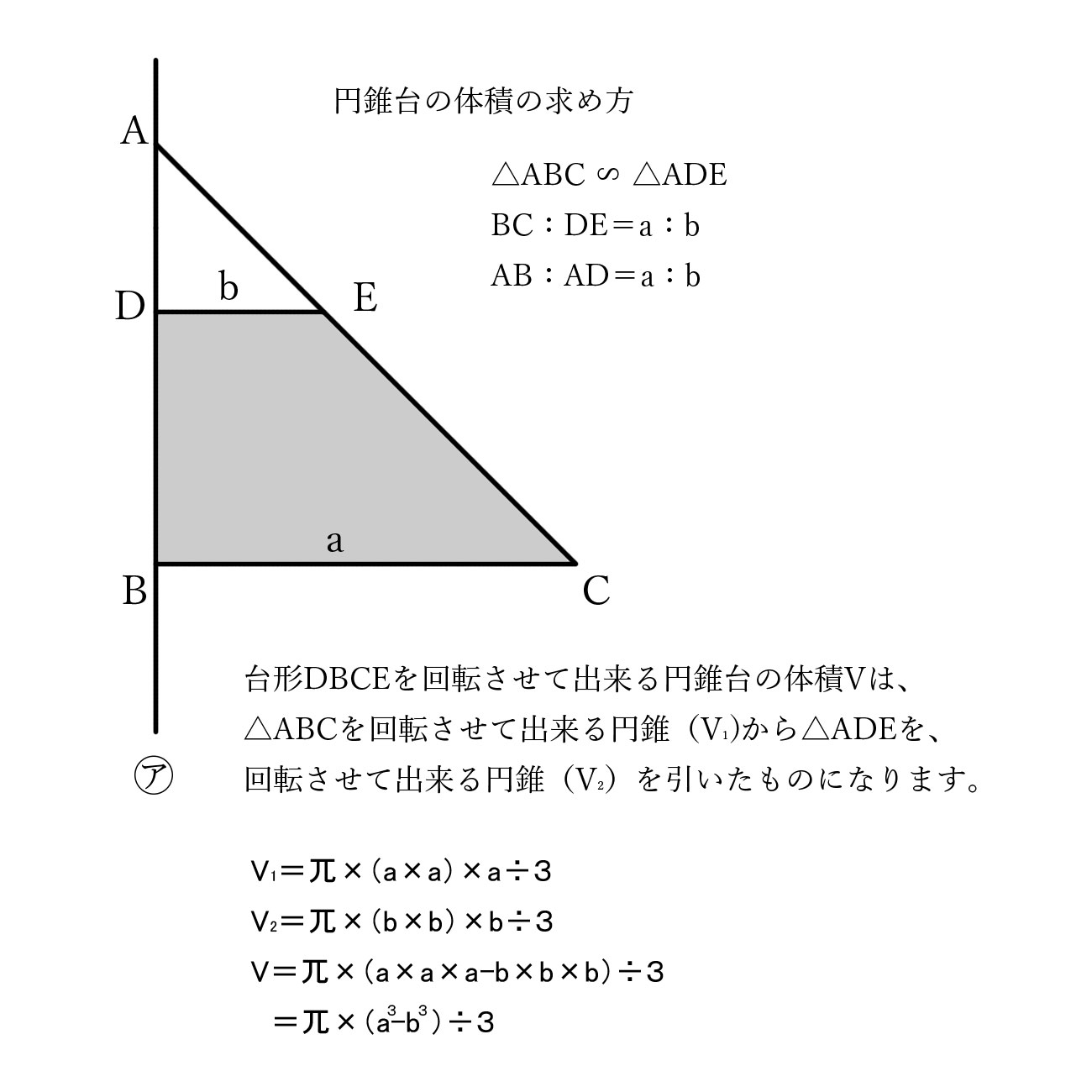
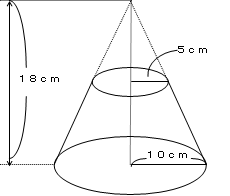
円錐台の体積を求めて,次にこれから中空の円柱の体積を引くとよい. まず,比例(相似)の関係から ABBC=ADDE → 34=6DE → DE=8 次に,円錐台の体積 π×6cm 2 ×8÷3=96π (cm 3)から上端の円錐の体積 π×3cm 2 ×4÷3=12π (cm 3)を引いて 84π (cm 3) 体積の求め方 重量の求め方 体積の求め方 立体 体積v 截頭円柱 角すい 球冠 楕円体 楕円環 交叉円柱 中空円柱(管) 截頭角すい 球分 円環 円すい 球 球帯 樽形 重量の求め方 12/3/19 2149 3 3 回答 円錐台の体積の求め方を教えてください。 円錐台で、上底の半径R(面積S)、下底の半径r(面積s)、 高さhのみが分かっている(元の大きな円錐の高さHはわからない)とき、 かつ公式V=(h/3) (S+√Ss+s)が 円錐台の体積の求め方
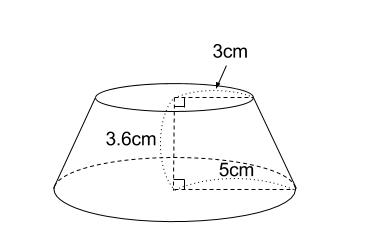
円錐の体積や表面積を求める際にも、円柱の体積や表面積の求め方が大きく関わります。ここでは円柱の体積の求め方を見ていきましょう。 「円柱」の体積を求めてみよう! 例題 底面の円の半径が 3cm 、高さが 8 cm である円柱 円錐 台 体積 求め 方 = 角錐上面積 球体 v = 体積 a = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体円錐の体積の問題数i求め方の違いについて ohを高さとする円錐がある。 円錐台の体積の求め方 円錐台の体積の求め方についての質問です。 上底の半径=3 下底の半径=4 高さ=3 円周率=π この場合、大きな円錐の体積-小さな円錐の体積 という考え方や円錐 台の公式がある (正解は37π)ことは知っています。
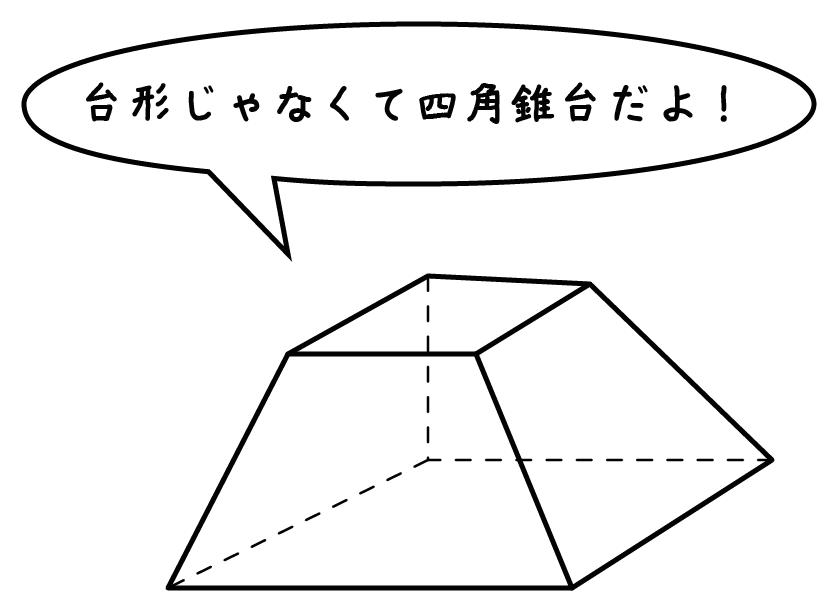
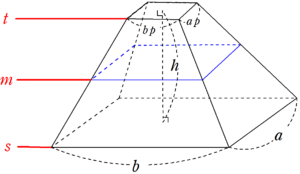
正四角錐台の体積の求め方の公式 を紹介するよ。 よかったら参考にしてみて。 台形の体積(正四角錐台)の求め方の公式!? 正四角錐台の下の1辺がa、上の辺がb、高さをhとしよう。 体積は、 1/3 h ( a^2 ab b^2) で計算できちゃうんだ。 つまり、(体積の概念の確認)「体積はこれに水がいっぱい入 った量だね」 円柱 円錐 <体積 たいせき > ←3倍(×3) 1/3 倍(×1/3)→ (上図の→←を指しながら) 2つが同じ底面積,高さであることを確認。 「円柱の体積は円錐の体積の3倍,×3。体積 V = 1 3 π ( r 1 2 r 1 r 2 r 2 2) h



Studydoctor相似比と体積比 円錐台 中学3年数学 Studydoctor
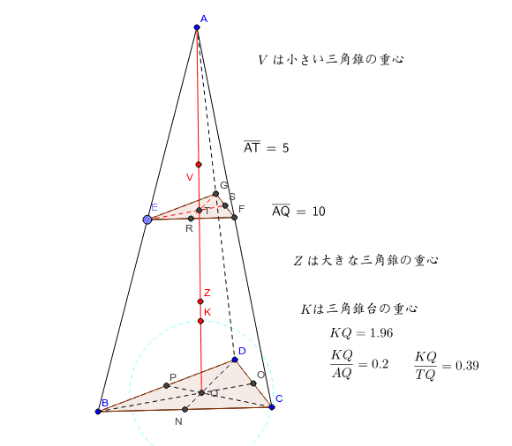



三角錐台の重心 Geogebra
問題図のような円錐を、Oを中心に転がすと、 $\textcolor{green}{3}$ 回転してもとの位置に戻りました。 円錐の母線の長さを求めなさい。 $3$ 回転ということは、中心がOである 大きい円の円周 は、 側面のおうぎ形 $\textcolor{blue}{3}$ 枚分の長さ と等しくなります。この円錐台の質量中心の底面からの高さを求めよ。 解答例 ( は円錐の体積)であり、 だから、 (2)切り取る前の直円錐の頂点を原点とし、底面への垂線方向を と求められる。円錐の体積を求める! 高さがわかれば体積を求めることができますね。 円錐の体積の求め方を確認しておくと こうでしたね。 コレに当てはめて考えていきましょう。 底面積は円の面積公式 に当てはめて となるので、体積は となりました。 三平方




円錐台の側面積の 1 1 3 がよくわかりません なぜ2条にするのですか Clear
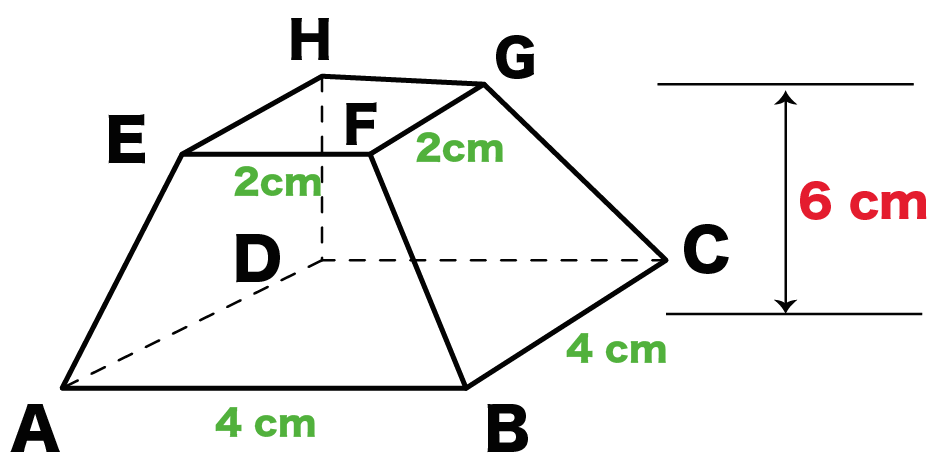



簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
円錐の体積の求め方を解説 こんにちはこんばんは! taraといいます。 6月も終わりを迎えようとしている今日この頃ですが、 空模様はまだまだ梅雨真っただ中ですね。 僕自身 円錐の体積=底面積×高さ÷3なので 求める円錐の体積=5×5×314×9÷3=2355(cm³) 答え 2355cm³ この円錐の展開図の側面になる扇形の中心角30°のとき、この母線の長さを求めなさい という問題がありました! 宿題 三角錐 四角錐 円錐 三角柱 四角柱 円柱の底面積と体積の求め方を教えてください。「円錐台の体積の求め方は、底面積aの円錐の体積-底面積bの円錐の体積です。 まず、




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ
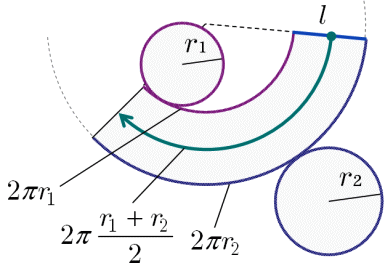



初等幾何 円錐台の側面積を求める 大人が学び直す数学
If playback doesn't begin shortly, try restarting your device You're signed out Videos you watch may be added to the TV's watch history and influence TV recommendations To avoid this, cancelX h = b h a − b ( a − b) h a − b = a h a − b となります。 したがって、大きな円錐の体積は、 π a 2 × a h a − b × 1 3 = π a 3 h 3 ( a − b) となります。 よって、円錐台の体積は「大きな円錐の体積」から「小さな円錐の体積」を引いたものなので、 ( a 3 − b 3) π h 3 ( a − b) = 1 3 π h ( a 2 a b b 2) このときBの体積が21cm3であったとすると、Cの体積はいくらか。 解説↓ 円錐Aを基準とすると、円錐A円錐台Bの高さは2倍で底面積は4倍となる。 体積は、円錐A:円錐A円錐台B=18と




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学
相似比を3乗することで求めてやることができます。 つまり 相似比がわかれば 体積比はすーぐに求めることができるということですね! それでは、さっきの円錐の問題を考えてみましょう。 円錐問題の考え方 円錐を2つに分けた図形の体積比を考えるの簡単公式台形の体積(正四角錐台)の求め方がわかる3 円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学 24 正答例と解説;円錐の体積と公式の問題、高さの求め方 下図の円錐の体積を、公式を用いて求めましょう。 上記の値を公式に当てはめれば良いので簡単ですね。 また下図の円錐の体積=15m 3 、半径=2mのとき、高さを求めてください。 円錐の高さは下式を用いて算定し




面積 体積 計算ツール 福井鋲螺株式会社 冷間鍛造 冷間圧造 ヘッダー加工の専門メーカー リベット 特殊形状パーツおよび省力機器の製造 販売




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ
高さ H と、高さ (H-h) の円錐の底辺の 半径 R と r は、 r/(H-h)=R/H より、 r=R(H-h)/H で、 なお、 r*H=R(H-h)、 H(R-r)=R*h ∴ H=R*h/(R-r) ・・・① また、 円錐台の底面積 S1 と上面積 S2 は、 S1=π*R^2 S2=π*r^2=R^2(H-h)^2/H^2 なお、 高さ (H-h) の円錐の体積 V0 は、円錐台の底面と上面の半径と高さから体積、側面積、表面積を計算します。 円錐台の体積 高精度計算サイト ゲストさん円錐台(えんすいだい、英 circular truncated cone )は、円を底面とした錐台である。 つまり、円錐を底面に平行な平面で切り、小円錐の部分を除いた立体図形である。 プリンの形は一般的には円錐台である。受験数学、特に日本の中学入試でよく出題される図形である。



1



緊急です この円錐の下の円の半径と円錐台の高さの求め方を教えて下さい Yahoo 知恵袋
円錐台の体積 円錐台の体積 円錐台の底面と上面の半径と高さから体積、側面積、表面積を計算します。 楕円錐の体積 楕円錐の体積 楕円錐の半軸と高さから体積、側面積、表面積を計算します。 楕円錐台の体積 楕円錐台の体積 楕円錐台の底面と上面の半軸と高さから体積、側面積、表面積を計算します。 球の体積 球の体積 球の半径から体積と表面積を計算し正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 四角錐台の体積 くさび形の体積 角錐台の体積 角錐の体積 直円柱の体積 一部が欠けた直円柱の体積 中空円柱の体積 斜切円柱の体積(体積の計算) 立体の体積を求めるには,体積の微分が断面積になることを利用します. すなわち,左端 a から座標 x までの区間にある体積を x の関数として V(x) で表し, x における断面積を S(x) とおきます. 上で復習した面積の求め方と同様にして




Mathematics 錐体の一部の体積 働きアリ
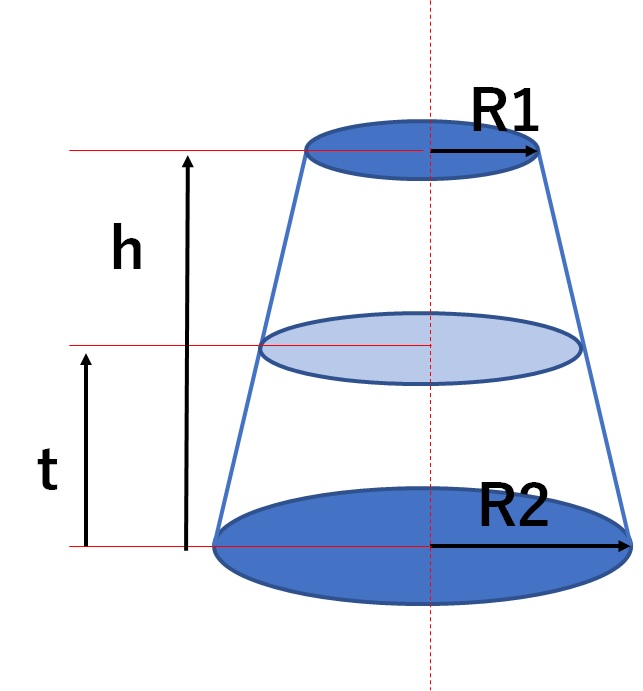



円錐台の体積を半分にする高さを計算 高精度計算サイト
円錐の表面積、中心角を求める問題を丁寧に解説! 円錐の展開図は以下のようになっているので、円錐の側面積は扇型であることがわかりますね。 この場合、母線から円錐の中心角を求めましょう。 半径が等しい扇形の面積は、弧の長さに比例する。そうすると、4次元錐体の体積は、b=0で、c=a/8 (3乗に比例する)だから、 となるはず。 s:へー。あれ、さっきの半球の体積は、底面が円で高さrの円錐の2倍ですよ。 円錐×2=半球 円錐×3=円柱 ということですか。



1




下の円錐台の体積の途中式まで教えていただきたいです Clear




公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成



体積の公式は 1分でわかる求め方と覚え方 一覧 三角柱 円柱 三角錐の体積



立体図形の体積




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




三角錐 体積 計算
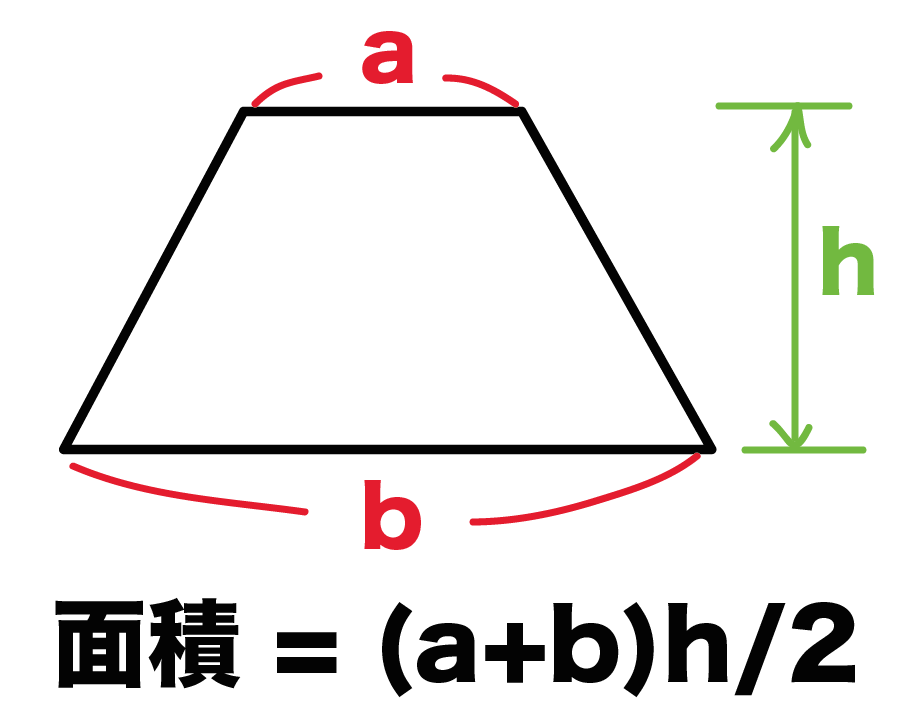



簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
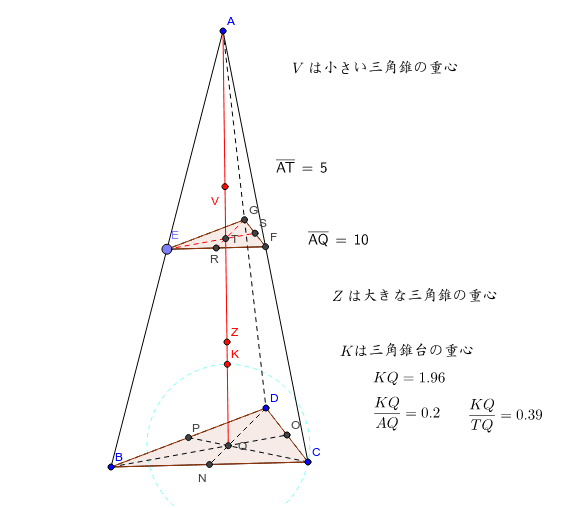



三角錐台の重心 Geogebra



立派な 台形 体積 求め 方




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ




空間図形14 円すい台の体積 Youtube



計算の部屋 冷間圧造用工具の設計 製作 株式会社エム ティ シィ




中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ



Newみんなの算数講座104 プリン 中学受験の算数知恵宝庫




簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
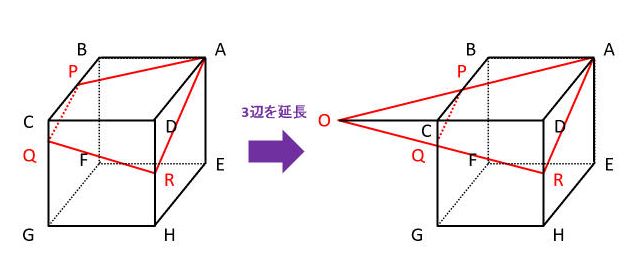



台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ




円錐の体積の求め方 公式と計算例



1



下のような四角錐台の体積の求め方をわかりやすく教えてください A 5b 3 Yahoo 知恵袋




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




相似比と体積比 円錐台 中学3年数学 Youtube




円錐台を傾けた時に 溢れる水の体積の計算 上辺の半径r 下辺の半 数学 教えて Goo




マンスリーミニ対策 円錐台 中学受験 プロ家庭教師 コージー先生の独り言




四角錐台の体積 高精度計算サイト



添付写真は 円錐台に穴が開いているタイプの図形です この体積 Yahoo 知恵袋




簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
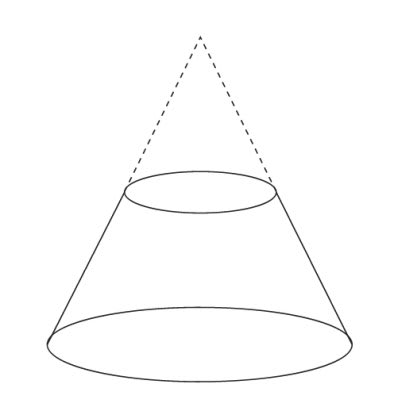



円錐を カット する 体積は どうなる 名寄 算数数学教室より




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット



3
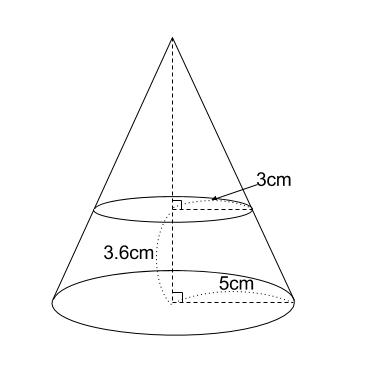



中学数学 相似な図形の体積比 中学数学の無料オンライン学習サイトchu Su
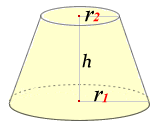



みんなの知識 ちょっと便利帳 円錐台の体積を計算する
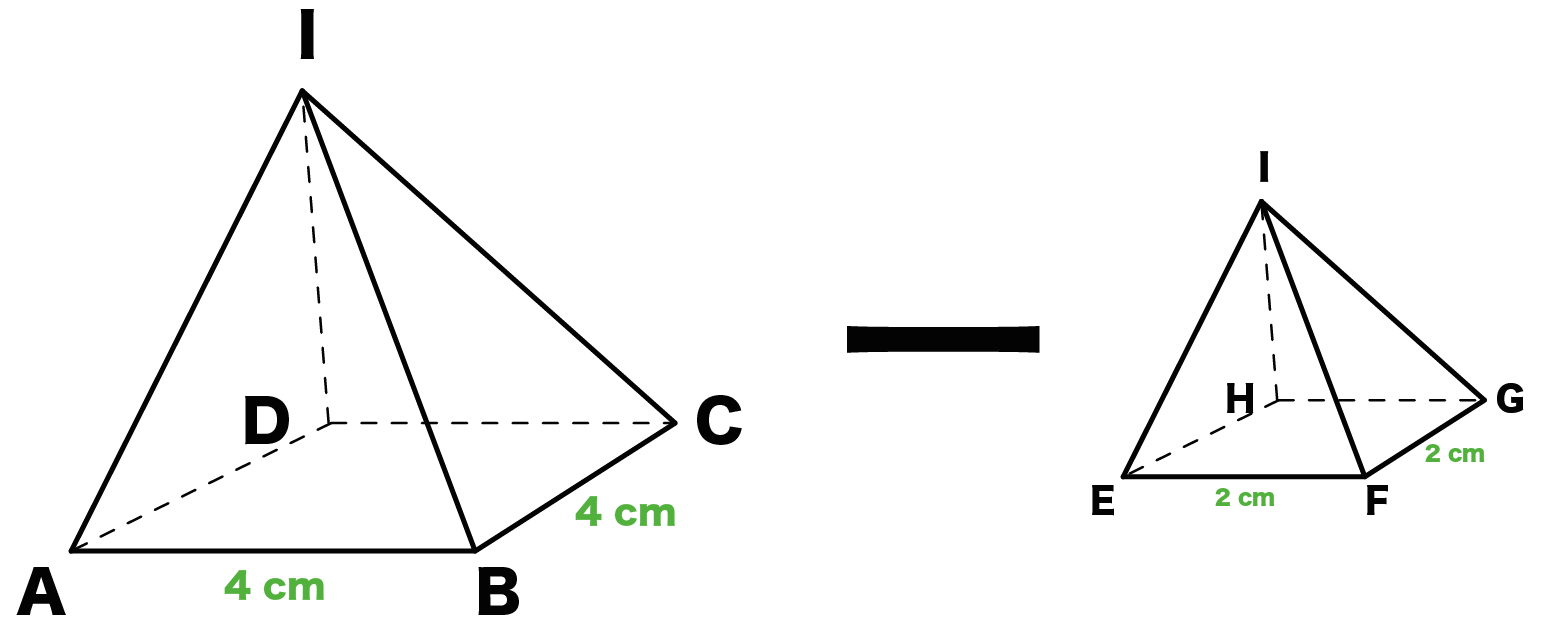



簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




M Sudo S Room 円錐台形の慣性モーメントに関する補足



私立中学 入試 問題の難問 偶然に 正解 セルフ塾のブログ



Math 円錐 円錐台と面積比 体積比 働きアリ




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学



円錐台の体積の求め方円錐台の体積の求め方についての質問です 上 Yahoo 知恵袋



一般的なプリンの体積の求め方 地底たる謎の研究室



簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



立派な 台形 体積 求め 方




円錐の体積ってなんであの公式なの Webty Staff Blog



円錐台の体積と高さについて回答をお願いします 図を添付してい Yahoo 知恵袋




中3 円錐台の体積 Youtube



シンプソンの公式 応用編 Fukusukeの数学めも




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



立派な 台形 体積 求め 方



体積 円錐台の体積を求める 子供に教える算数のツボ




Solidworksで円錐台や円錐の作り方は



中学数学 相似な図形の体積比 中学数学の無料オンライン学習サイトchu Su




円錐の体積ってなんであの公式なの Webty Staff Blog



図のような円錐台の体積を求めるにはどのような計算をすればよいか教えてください Yahoo 知恵袋
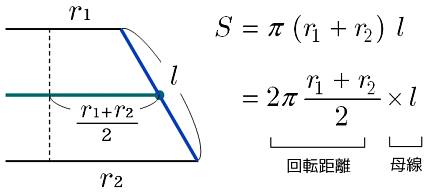



初等幾何 円錐台の側面積を求める 大人が学び直す数学



三角錐 体積 計算



角錐台の体積 高精度計算サイト




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット
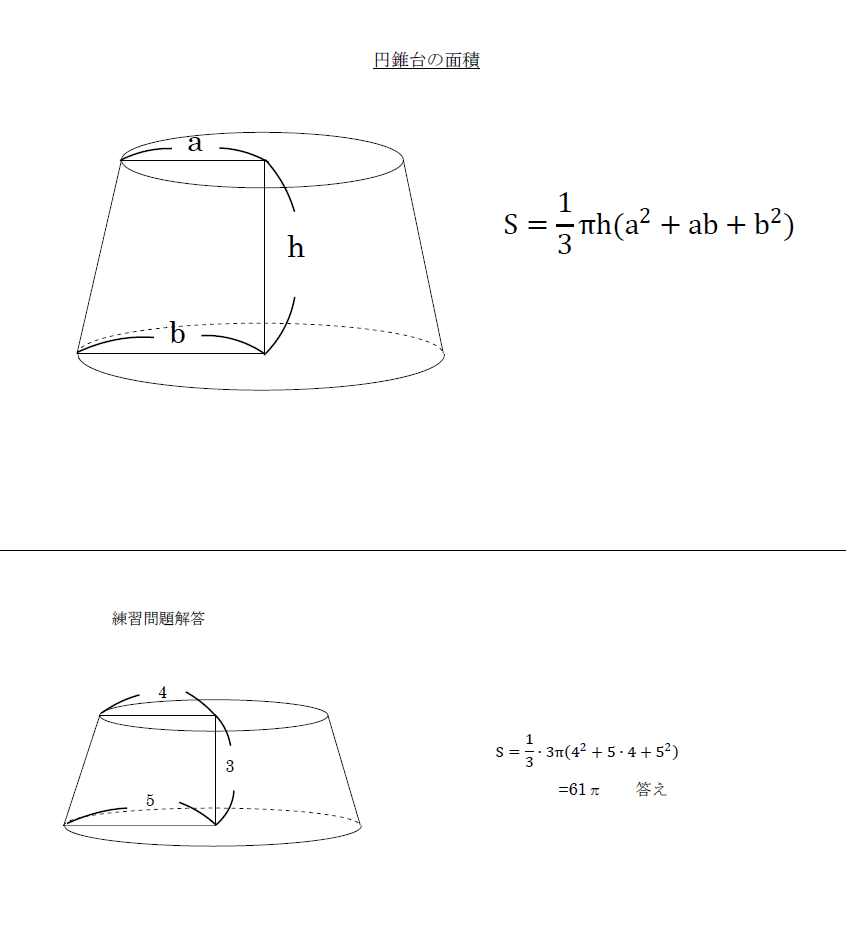



空間図形の体積 円錐台 の解法 中学 受験 定期試験 数学解き方集 裏技 解法



円すい台側面積の公式を導く




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




円錐台の体積 側面積 香料ゐっすゐの夢




裏技 プリン型の立体の体積 一瞬で求められますか Youtube



円錐台の公式 体積 面積 数学 エクセルマニア




立派な 台形 体積 求め 方



楕円錐台の体積 高精度計算サイト
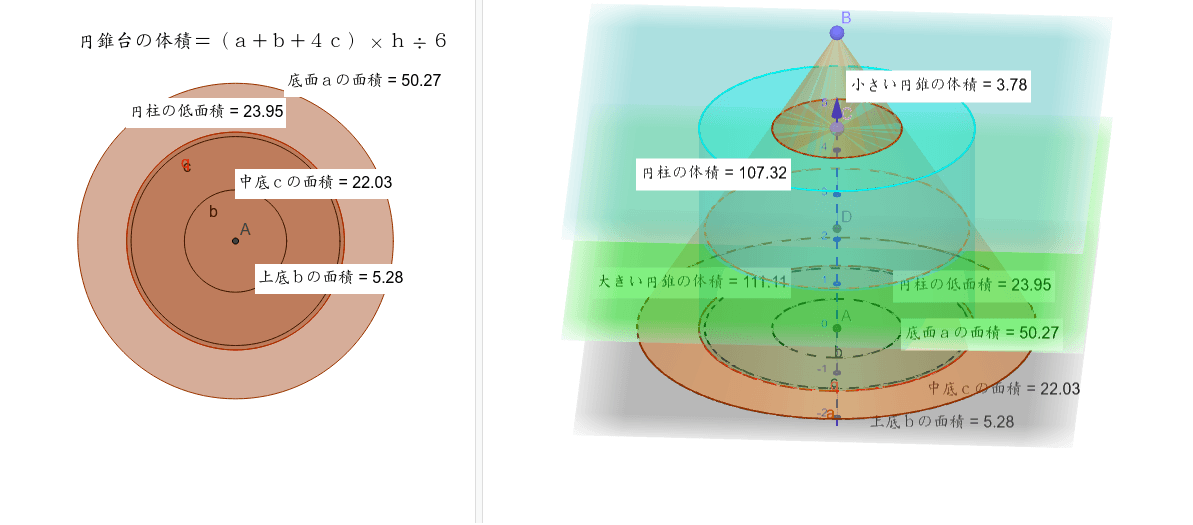



シンプソンの公式 Geogebra




円錐の体積が円柱の1 3なのはなぜなのか



Math 円錐 円錐台と面積比 体積比 働きアリ




公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成




円錐台 Wikipedia
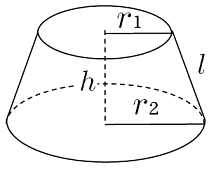



初等幾何 円錐台の側面積を求める 大人が学び直す数学




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




円すい 円錐 の体積の求め方と問題 小学数学 Irohabook




2000年 東京大学 文科 前期 数学 第1問 ますいしいのブログ




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




中3 三角形の相似 円錐の体積比 日本語版 Youtube



地図の体積計測




三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学




公式を図解 すい体の体積 円すいの表面積の求め方



相似比と体積の計算 円錐台 三角錐台 中学3年数学 Youtube
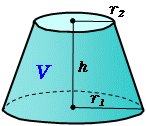



円錐台の体積 高精度計算サイト




高さの分からない円すい展開図 どうやって立体の体積を求めるの



地図の体積計測




中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ



Studydoctor相似比と体積の計算 円錐台 三角錐台 中学3年数学 Studydoctor



四角錐台の公式 体積 側面積 表面積 数学 エクセルマニア
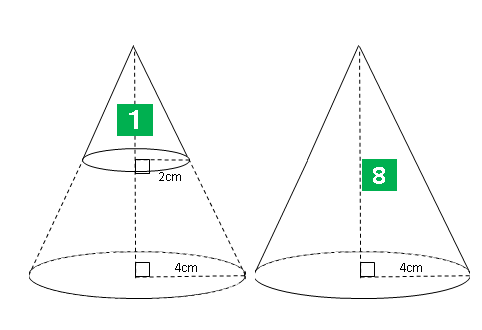



相似と体積比 3 ネット塾
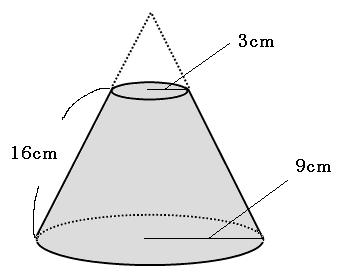



円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる




相似と体積比 3 ネット塾



0 件のコメント:
コメントを投稿