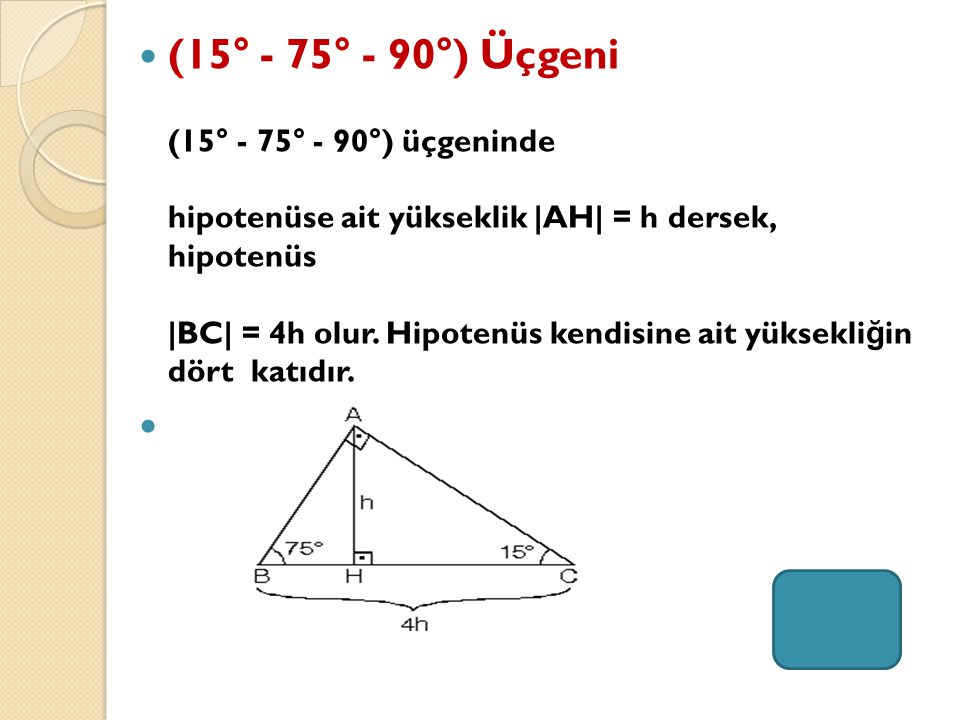
Alınan herhangi bir dik üçgenin kenarları arasındaki ilişkiye denir Bu ilişkiye göre;15 75 90 üçgeni özelliklerinin ispatıDaha fazla ispat için http//wwwozelderscicom/matematikformullerininteoremlerininhtmlSitemizi ziyaret e 15 75 90 üçgeni özellikleri çoğu zaman dik bir üçgene dikme indirildiğinde ortaya çıkar Görselden de gördüğünüz gibi dik üçgenin, dik açısından tabana doğru bir dikme indirilmiş Daha sonra karşımıza iki adet 15 75 90 üçgeni çıkmış Yukarıdaki 15 75 90 üçgeni özellikleri, bu üçgenlerde kullanılarak sorunun doğru yanıtı bulunur
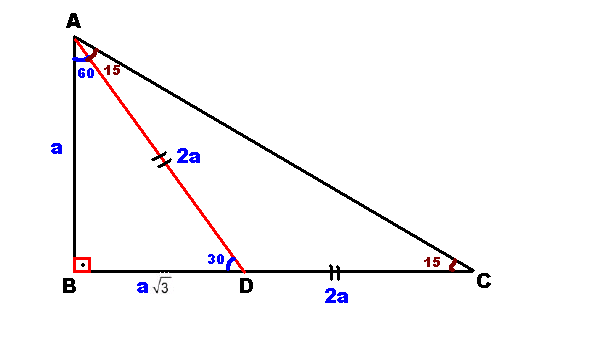
15 75 90 Ucgeni 2 3 Ispat
75 15 90 üçgeni formülü
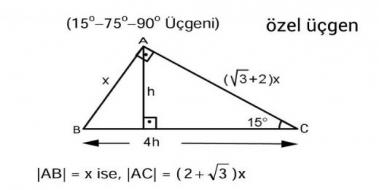
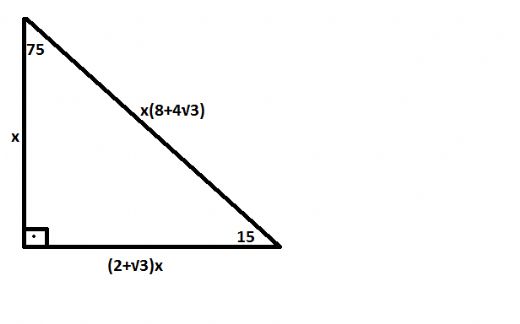
75 15 90 üçgeni formülü- 15 75 90 özel üçgeninin altın kuralı 15 derecenin karşısı 1 birim ise 75 derecenin karşısı √3 2 birim olmak zorundadır Hipotenüs ise 8 4√3 olarak hesaplanır Yukarıdaki kuralı uygulayabilmeniz için 15 75 90 özel üçgeninin var olması gerekiyor 15° 75° 90° üçgeni, Özel bir üçgendir Matematikte özel kavramı;
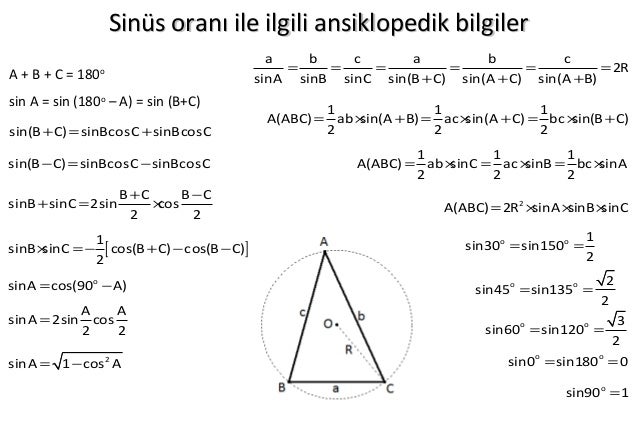



Ucgen Ve Cokgenlerle Ilgili Soru Ve Alistirmalar
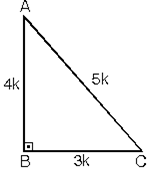
75 dereceyi 1560 derece olacak şekilde ayıran bir kenar çizip karşı dik kenar ile birleştirirsek, bir tarafta ikizkenar üçgen diğer tarafta üçgeni oluşur ve kenar uzunlukları arasındaki bağıntı ezberlenmemiş olur dik kenarlar arasındaki bağıntıyı hatırlayacak olursak, 15 in karşısındaki kenar "a" ise 75 in karşısındaki kenar "2aakök3" aynı yolla 2215 75 90 üçgeninde hipotenüse indirilen yükseklik hipotenüsün dörttebiridir kuralının ispatını bu videoda bulabilirsiniz Özel üçgenlerden bilinmesi gereken üçgenlerden bir tanesi de 15 75 90 üçgenidir Bu üçgenin bilinmesi soruların çözülmesi açısından basitlık sağlamaktadır 15 75 90 üçgeni bir dik üçgendir Her üçgende olduğu gibi iç açıları toplamı 180, dış açıları toplamı ise 360 derecedir Bu dik üçgende kenar uzunlukları için Pisagor teoremi uygulanmaktadır 15 75
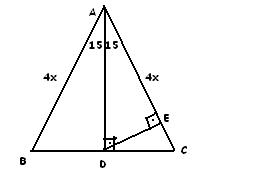
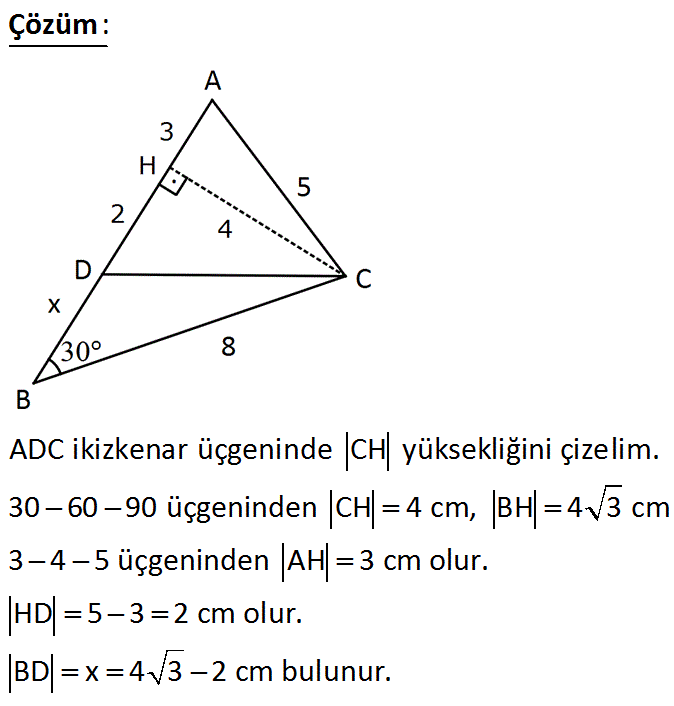
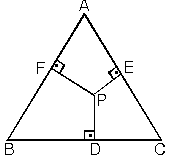
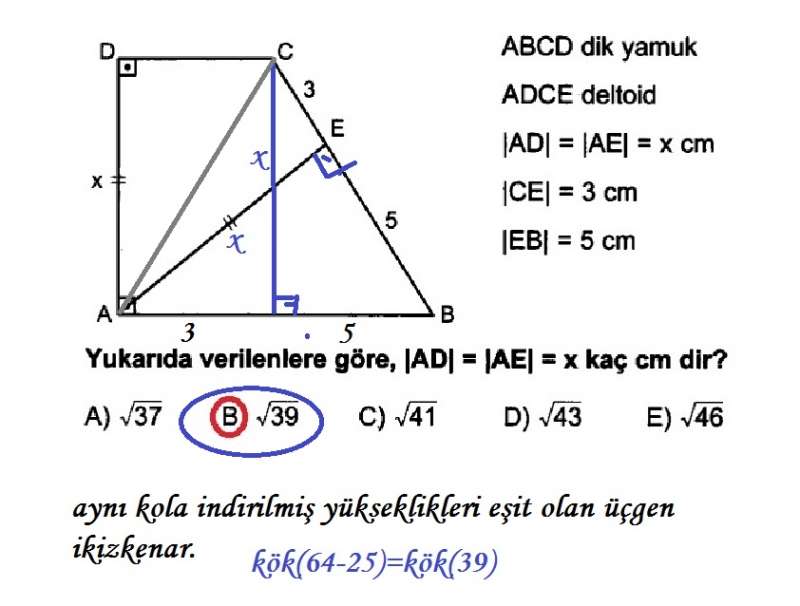
AD C üçgeni 15 75 90 üçgenidir 15 75 90 üçgeninde hipotenüse inen yükseklik, hipotenüsün 4' te 1'i dir 4 2 x 2 cm bulunur 4 12 ABC eşkenar üçgen, AB // AD AE AD ED 2 cm Yukarıdaki verilere göre, BE x kaç cm dir? 90 75 15 üçgeni, Müfredat tarafından belirlenen kurallar ve işleyiş tablosuna göre genellikle daha çok sayısal ve eşit ağırlık öğrencilerinin öğrenmesi gereken konular arasındadır Bunun sebebi ise tamamen seçtikleri bölümden kaynaklıdır İlerideki girecek oldukları sınavlarda ancak kendi bölümlerindeki konulara hakim oldukları kadar başarı sergilerler Çünkü 75 15 90 Üçgeni;
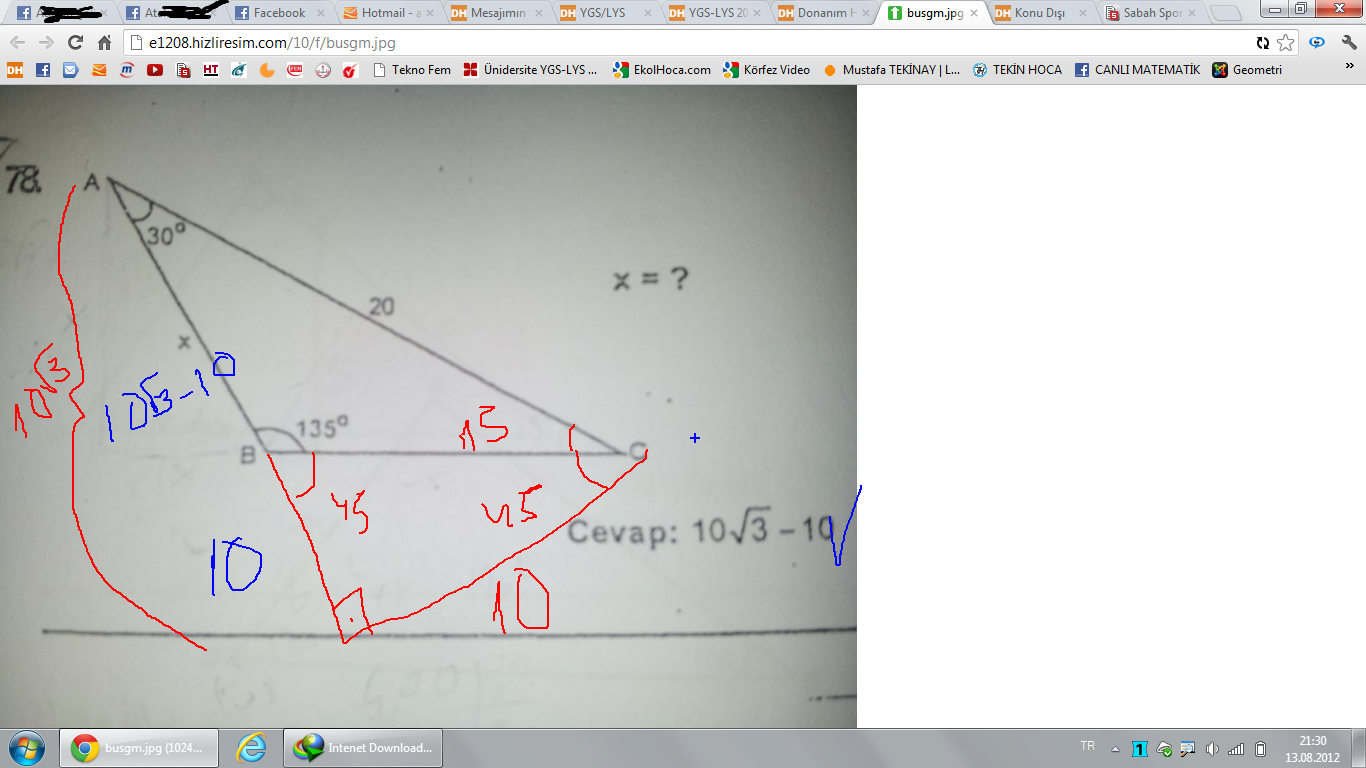
A) 2 3 4 B) 2 3 6 C) 4 3 2 D) 4 3 4 E) 4 3 6 wwwmatematikkolaynet Çözüm 15 75 90 üçgeninden AD 8 4 3 olur ABD ve HAD üçgenleri benzer üçgenlerdir 15 75 90 üçgeni Matematiğin geometri dalının özel formülü olan özel üçgenlerinden birisidir15 75 90 üçgeni kendine has kuralları olan bir üçgendir ve kuralları değişmez zaten değiştirildiği takdirde açı ve uzunluklarından ötürü özel üçgen olmaktan çıkar Bazı özel formül ve kurallar bizlere soru ve problem çözümünde oldukça fayda sağlar ve biziDik olan kenarların kar toplamları hipotenüsün karesine eşit olur




Kisa Yollar 2 15 75 22 5 67 5 Derecenin Trigonometrik Degerleri Youtube




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz
15 75 90 üçgeninin kenarları arasındaki bağıntının nerden geldiğinin ispatını bu videoda izleyebilirsinizTeoremin kendine has özelliklerinin olmasıdır Bu özellikler başka hiç bir teoremde yada cisimde bulunmamasıdır En önemlisi de teoremi çözebilmek için bazı kuralların ve formüllerin kullanmasıdır Üçgenlerin 3 adet kenarı ve 3 adet açısı vardırQuote Orijinalden alıntı brknzbz üçgeninde şu bağıntılar vardır 1 (kök31)k (kök31)k (2kök2)k sırasıyla derecelerin karşılarındaki kenarların aralarındaki bağıntıdır bu 2 15 derecenin hemen yanına doğru bir doğru parçası indirerek ikizkenar üçgen oluşturup (1515 derece şeklinde) küçük bir 0 ve üçgeni oluşturmak




Dik Ucgenler Pisagor Teoremi Konu Anlatimi Soru Cozumleri Ders Notu 9 Sinif Matematik Tyt




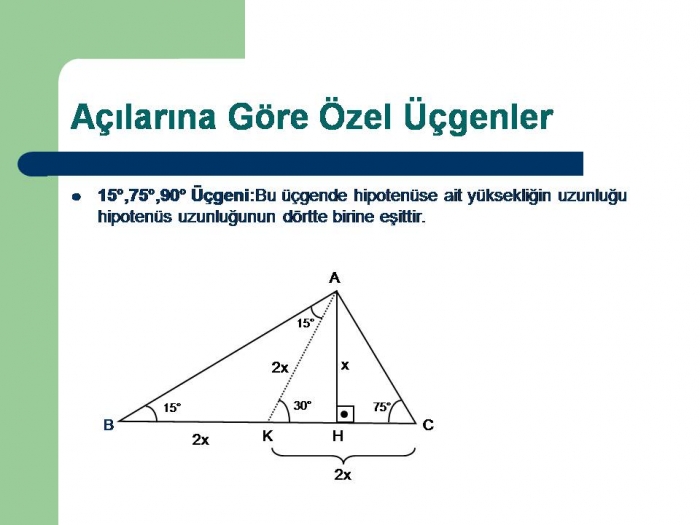
75 15 90 Ucgeni Acilarina Gore Ozel Dik Ucgenler
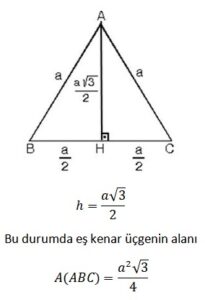
üçgeninde hipotenüse indirilen yüksekliğe h diyelim Daha Sonra Süper üçlüyü kullanmak için hipotenüsü iki eşit parçaya bölecek kenarortayı çizelim 3 adet üçgenimiz oluştu () () (0) 30⁰'nin karşısına hIç açılarından bir tanesinin açı derecesi 90 olan üçgenlerdir Çemberde ise çapı tam göre açı ölçüsü 90 derece olur Pisagor teoremi;Proof Without Words kitabından şahane bir sözsüz kanıtDaha fazlası MY VİDEO EĞİTİM SİTESİ'nde Misafir olarak giriş yapabilirsiniz Detaylar için wwwmustaf




Ucgenler Icin 76 Fikir Evde Egitim Matematik Geometri
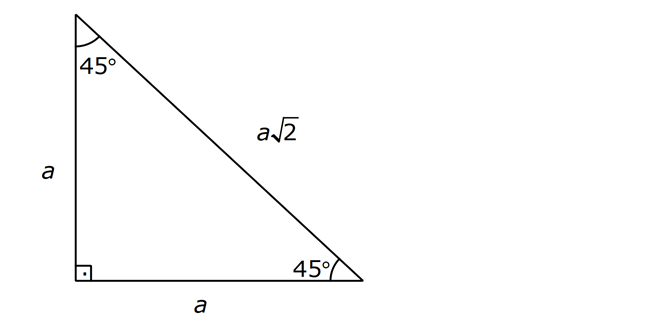



Ozel Ucgenler Konu Anlatimi
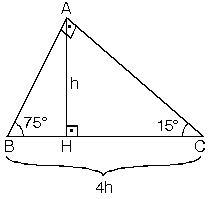
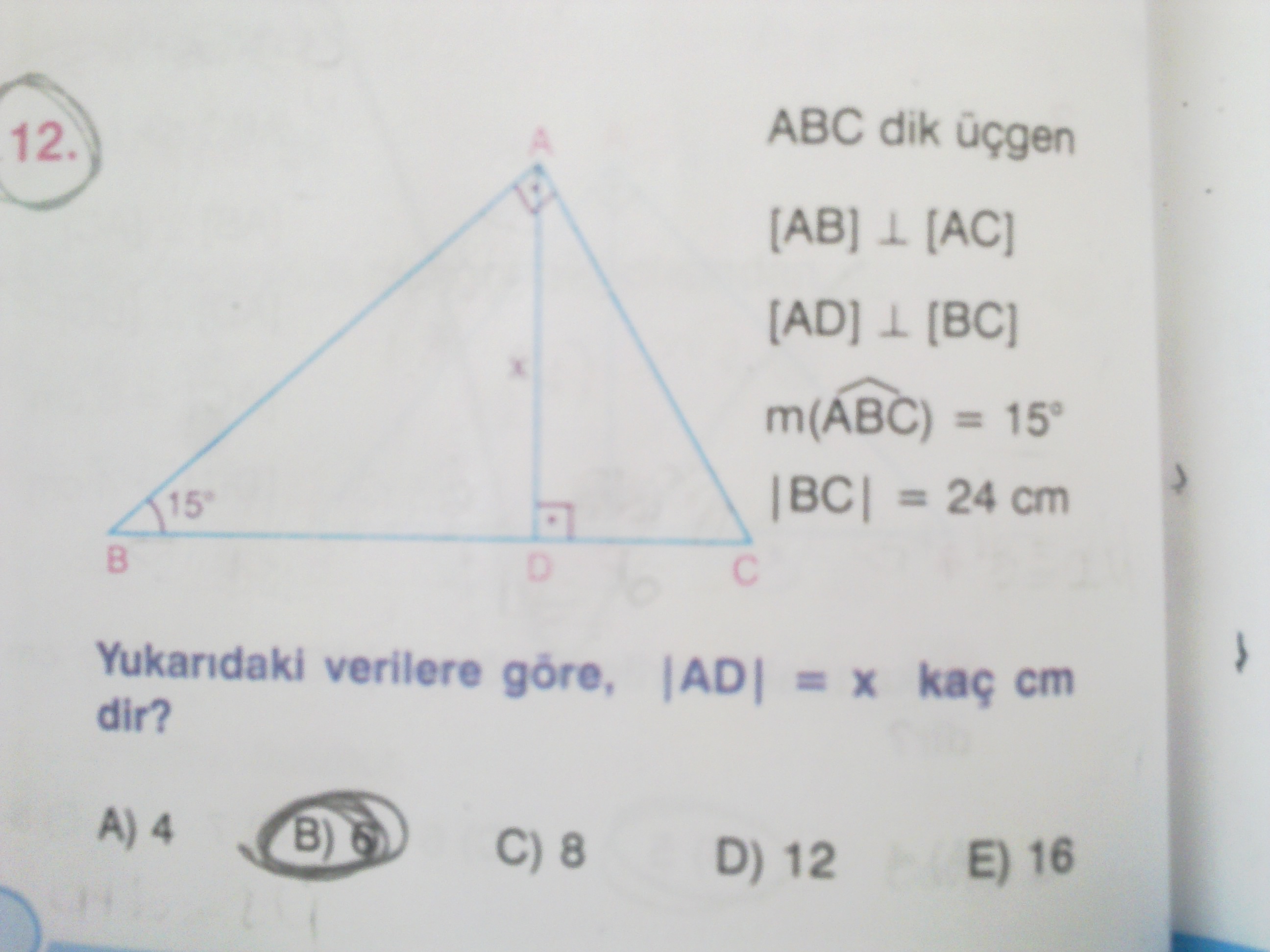
15 75 90 üçgeni ile ilgili bilmemiz gereken ve çok basit olan bir dikme özelliği vardır 15 75 90 üçgeni içerisinde 90 dereceden hipotenüse indirilen bir dikmenin uzunluğu hipotenüsün 4'te biri kadar olur Yani dikme ile hipotenüs arasında h 4h bağıntısı vardır Üçgenler geometride ve hayatın birçok alanında karşımıza çıkmaktadır Üçgenler konusu öğrencileri de çok ilgilendiren bir konudur Sınavlarda üçgenler Bir üçgende iç açıları toplamı 180 derece olduğu için diğer açı 1 = 15 işleminden 15 derece olarak bulunur Yani bu üçgen 15 75 90 üçgenidir Hipotenüsün uzunluğu bu kenara ait yüksekliğin 4 katı olduğu için 43 = 12 işleminden, hipotenüs uzunluğu ise 12 cm olarak karşımıza çıkar 2
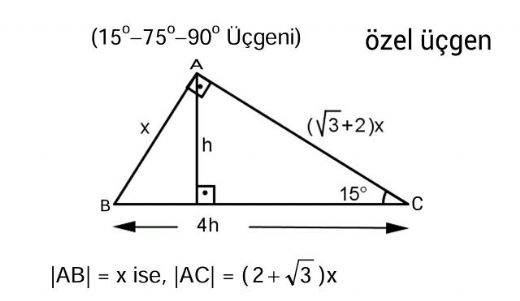



90 75 15 Ucgeni Ozellikleri



Www Mdpi Com 72 4292 11 6 605 Pdf
15 ve 60 olarak böldüğünüzde ise karşınıza bir 30 60 90 üçgeni ve de diğer tarafta kalan açıları 15 15 150 olan bir ikizkenar üçgen çıkacaktır bu durumda şöyle bir sonuç çıkar karşımıza 15 derecenin karşısındaki kenara a değerini verirsek, 75 derecenin karşısındaki kenar da 2aakök3 olacaktır 90'nın karşını da pisagor teoreminden hesaplayın, işiniz15 75 90 Üçgeni Geometri dersi için önemli özel üçgenlerden olan 15 75 90 üçgeni üçgenin sabit oranından gelmektedir Dik üçgen olan bu üçgende, diğer üçgenlerde olduğu gibi 15 75 90 üçgenin de kenarları arasında sabit oran bulunmaktadır Bu bakımdan kenar bağlantılarını bilmek üçgenin tanımının da yapılmasını sağlayacaktır 15 75 90 üçgeni içinde 90




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz




Matematik Formulleri Ozel Ucgenler 15 75 90 Ucgeni Wattpad




15 75 90 Ucgeni Ozelliklerinin Ispati Youtube




15 75 90 Ucgeni Ozelliklerinin Ispati Youtube



15 75 90 Ucgeni Kenar Bagintisi Ispat




15 75 90 Ozel Ucgeninin Kenar Bagintilari Nedir Eodev Com



1



Populer Icerik




Index Of Wp Content Uploads 18 05




15 75 90 Ucgeninde H 4h Kuralinin Ispati Youtube
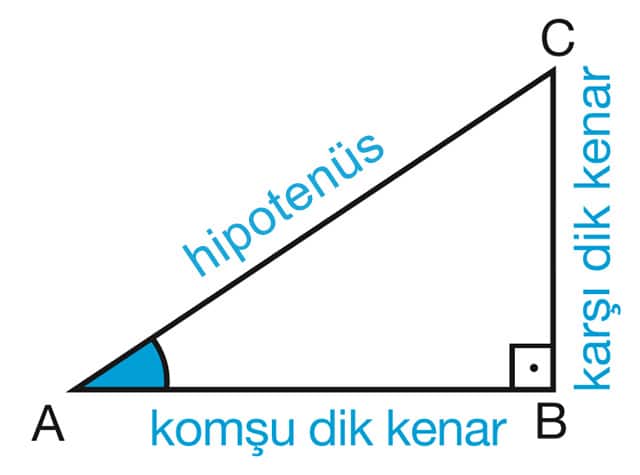



Trigonometri Dik Ucgenlerdeki Trigonometrik Oranlar Matematikciler Com
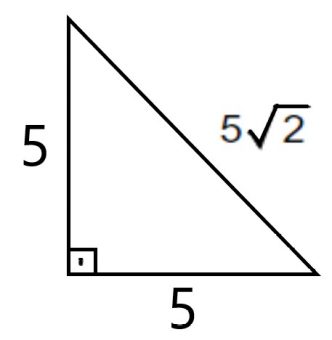



Pisagor Bagintisi Konu Anlatimi Pisagorun Uygulamalari




Pdf Dynamical And Statistical Models Of Vertebrate Population Dynamics
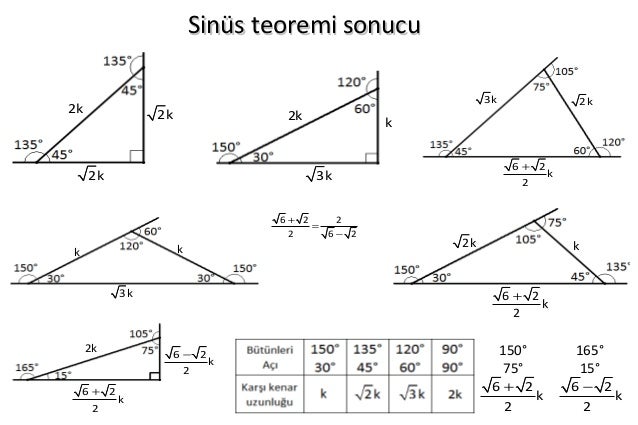



75 15 90 Ucgeni Kenarlari シモネタ




Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




15 75 90 Ucgeni Eodev Com




15 75 90 Ucgeni Ispati




Ucgenin Alani Nasil Bulunur Ucgen Alan Formulleri Ve Cesitleri Bilgeniz Com
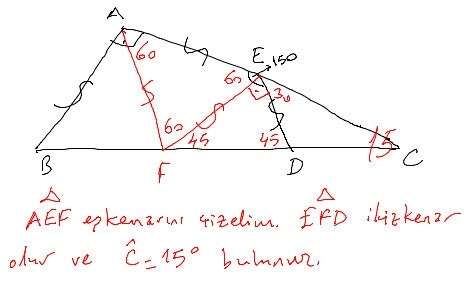



Acill Ozel Geometri Sorusu



45 45 90 Ucgeni Matematikce




Hd限定75 15 90 Ucgeni Ozelligi




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz
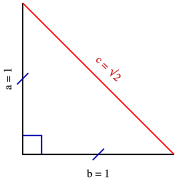



Dik Ucgen Vikipedi




Geometri 15 75 90 Ucgeni Nasil Olur Youtube
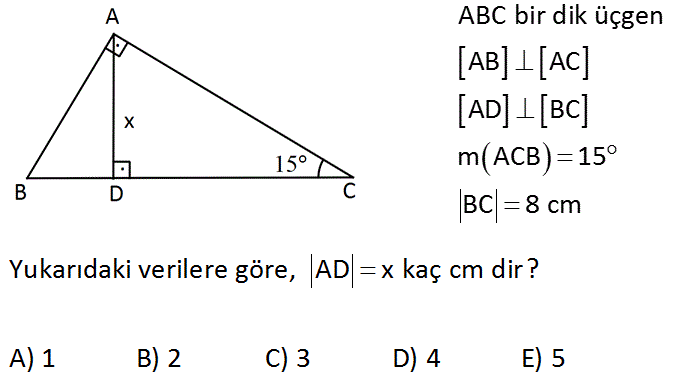



15 75 90 Ucgeni




15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz




15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz




Dik Ucgen 16 15 75 90 Ucgeni Temel Matematik Matematik Felsefesi Evde Egitim



Ucgen Ve Cokgenlerle Ilgili Soru Ve Alistirmalar



1




Ucgenler Ozel Ozel Ucgenler Ucgen Cesitleri Ucgenlerin Ozellikleri Pisagor Bagintisi Ile Ilgili Konu Anlatimlar Matematik Dersi Ile Ilgili Konu Anlatimlar Ornekler Cozumlu Sorular




Ucgen Ve Cokgenlerle Ilgili Soru Ve Alistirmalar
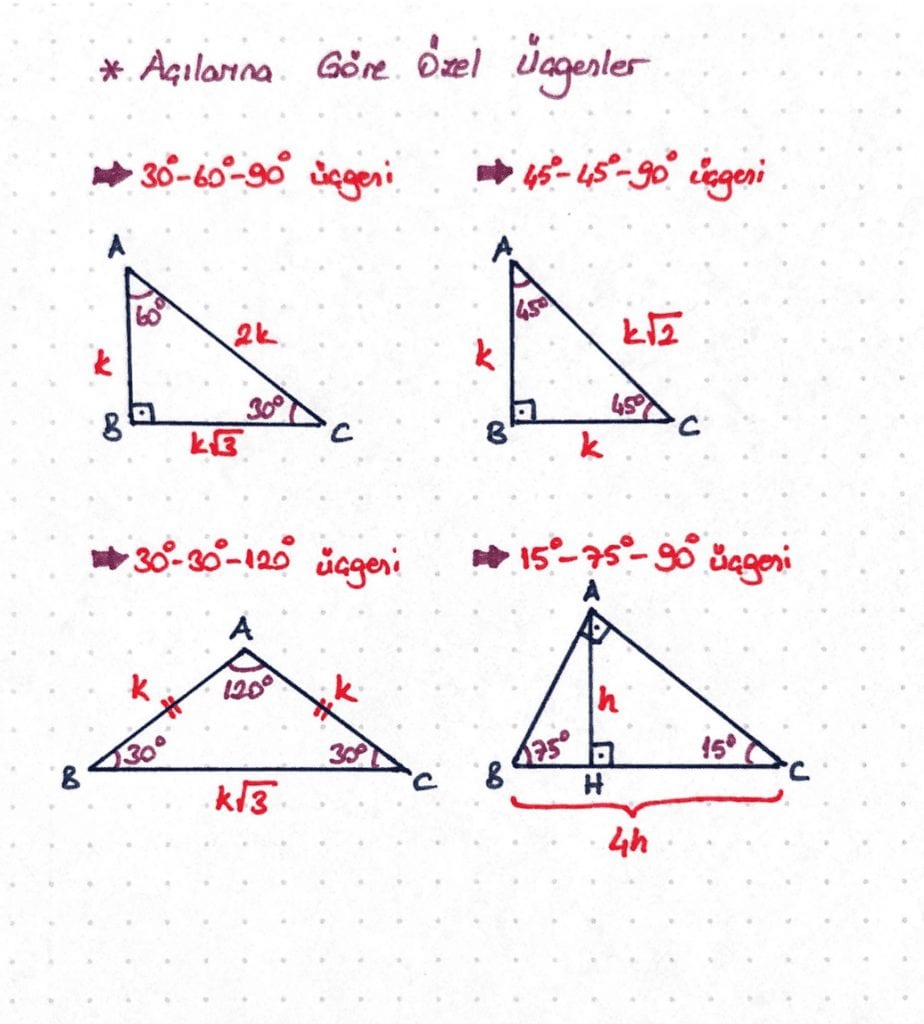



15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz




15 75 90 Ucgeni Ispati Not Bu



En Hizli 30 60 90 Ucgeni Ozellikleri



Ailles Langley Hakkinda Matematik Kafasi




Ucgenlerde Uzunluk Matematik Ve Geometri
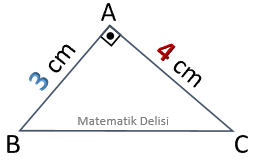



2 Kok 5 3 Ucgeni
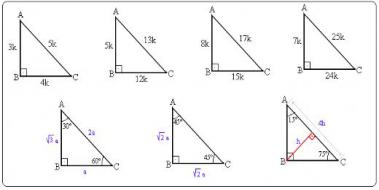



Ucgen Gen Tr Gizlilik Politikasi Www Ucgen Gen Tr Sitemizi Ziyaret Ettiginiz Ve Gizlilik Ilkemizi Okudugunuz Icin Tesekkur Ederiz Ziyaretiniz Esnasinda Sadece Ziyaret Saatiniz Ve Ziyaret Ettiginiz Sayfalarin Kaydi Tutulmaktadir Gizlilik Ilkemizin Temeli Basit Ve




画像をダウンロード 75 15 90 Ucgeni Ozellikleri 子供のためのちょうど着色ページ




Geometri Formulleri Sezgin Oner Matematik Yayinlari Facebook




Ozel Matematik Dersi Bursa 帖子 Facebook



En Hizli 30 60 90 Ucgeni Kurallari
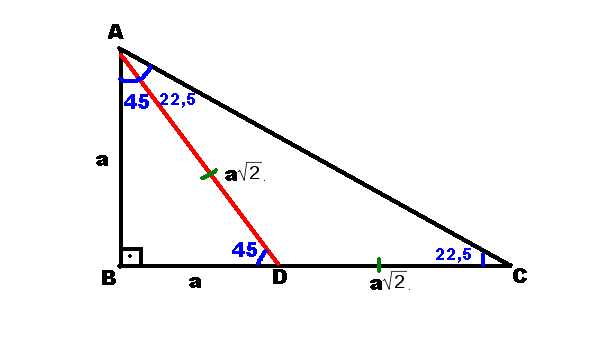



22 5 67 5 90 Ucgeni 1 2 Ispat
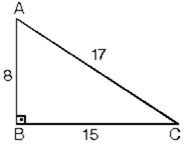



Dik Ve Ozel Ucgenler 1




Acilarina Gore Ozel Ucgenler 15 75 90




15 75 90 Ozel Ucgeni Ozellikleri




15 75 90 Ucgeni Ozellikleri Ve Kurali Soru List




1000以上 75 15 90 Ucgeni Kenarlari




15 75 90 Ucgeni Ozellikleri Ve Kurali Ogrenci Yardim




15 75 90 Ozel Ucgeni Oluyor Ama Ben Sadece O Ucgenin Yukseklik Le Ilgili Ozelligini Biliyorum Baska Eodev Com




Ispat 15 75 90 Ucgeni Tyt Geometri Ozel Ucgenler Youtube



Www Nanomatematik Com Wp Content Uploads 21 03 7 Sinif 5 Unite Birlestirilmis Matematik Pdf




Dik Ucgen Wikiwand
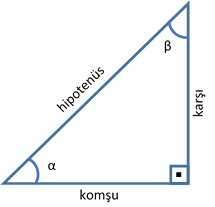



Dik Ucgende Trigonometrik Hesaplamalar




15 75 90 Ucgeninde Alan



15 75 90 Ucgeni Oklid Dikten Dik Ahbaci Matematik Geometri Ve Turkce Blogu Dgs Ales Kpss



Ozel Ucgenler Ppt Video Online Indir



Dik Ve Ozel Ucgenler 1




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz




Dik Ucgen 17 22 5 67 5 90 Ucgeni Evde Egitim Matematik Ders Calisma Ipuclari



Www Nanomatematik Com Wp Content Uploads 21 03 7 Sinif 5 Unite Birlestirilmis Matematik Pdf



Ozel Ucgenler



最新 75 15 90 Ucgeni シモネタ



100以上 75 15 90 Ucgeni Ozelligi シモネタ



15 75 90 Ucgeni Uludag Sozluk




30 60 90 Ucgeni Ve Ozellikleri Not Bu




Dik Ucgen Formulleri Nelerdir




Dik Ucgen 5 45 45 90 Ucgeni Geometri Metin Hocam Youtube



15 75 90 Ucgeninin Ozellikleri Nelerdir



1




15 75 90 Ucgeni Not Bu



Ozel Ucgenler Konu Anlatimi




15 75 90 Ucgeni Kurali Nedir 15 75 90 Ozel Ucgeni Ozellikleri Ve Ornek Sorular Egitim Haberleri




Ozel Ucgenler Not Bu




15 75 90 Ucgeni Webders Net



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




15 75 90 Ve 22 5 67 5 90 Ucgenleri Daha Once Hic Ygs De Cikti Mi




15 75 90 Ucgeni Pow Bylge



Cozemedigim Sorular



En Hizli 30 60 90 Ucgeninin Kurali




15 75 90 Pisagor Ucgeninin Formulunu Bilen Biri Var Mi Eodev Com




15 75 90 Ucgeni Kurali Nedir 15 75 90 Ucgeni Ozellikleri Ve Sorulari




15 75 90 Ucgeni 2 3 Ispat



1




15 75 90 Ucgen Ozelligi Ve 5 Ornek Cozum Youtube



15 75 90 Ucgeni




15 75 90 Ucgeni Akilli Geometri



15 75 90 Ucgeni Ozellikleri




8 Sinif Ucgen Esitsizligi Ve Aci Kenar Bagintilari Konu Anlatimi Matematikciler Com




Ucgende Acilar Cozumlu Sorulari Ve Problemleri Matematik Ogretmenleri




Ozel Ucgenler Ders Notu Konu Anlatimi Ders Notu
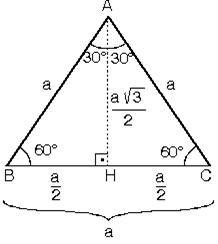



Dik Ve Ozel Ucgenler 1




Dik Ucgen Wikiwand




15 75 90 Ucgeni Ozelliklerinin Ispati Youtube




15 45 1 Ozel Ucgeni Var Mi Varsa Kurali Nedir Eodev Com



0 件のコメント:
コメントを投稿