二等辺三角形の角度を求める問題を練習したいですっ★ ってことで、今回の記事では二等辺三角形の角度を求める問題について解説していきます。 角度を求める問題は、図形の性質を覚えてしまえば楽勝! だから、この記事を通して二等辺三角形
上 中学 3 数学 757520-中学3��学 平方根
中学生向けの数学教材を無料ダウンロードできる総合サイト 空間図形 資料の整理 中2数学 式の計算 連立方程式 1次関数 平行と合同 四角形 確率 中3数学 かずのかず こちらで 確認してくださいね 中3数学「式の展開 (乗法公式)」の問題 どこよりも簡単な解き方・求め方 前回「式の展開」を学習しました 「多項式×多項式」の問題は、1つ1つ計算すれば、必ず答えを出すことができます ただ、特別な形の展開・因数分解 中3数学展開の公式のやり方は? 問題を使って徹底解説! LINE 今回は中3で学習する展開の計算について解説していきます! この展開の計算とは、今後学習していく単元で必須となってくる計算方法の1つです。 しっかりとマスターし

中学3年生 数学 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
中学3数学 平方根
[10000ダウンロード済み√] 証明 数学 問題 111991-中2 数学 証明 問題 応用
授業実践記録(数学) 「証明のしくみについて学ぼう」 愛媛県松山市立中学校 教諭 単元:4章 図形の調べ方(2節 証明) 問題1次のことがらが正しければ を,正しくなければ×を記入せよ。都立入試数学では例年2問程度証明問題が出題されています。 令和2年度(年度)では大問2の〔問2〕が数式を用いた証明問題。 大問4の〔問2〕①が三角形の合同を証明する問題でした。 証明は解答が面倒なので差がつきやすい!数学史において「証明」の果たしてきた役 割は大きい。また,杉山(1975,1986)から示唆 されるように,「証明」は数学教育において教 育的に意義ある学習内容である。一方,ホー ガン(1993)に代表されるように,コンピュー

中学数学の図形の合同の証明の問題です 2 がわからないのでわかる人いますか Clear
中2 数学 証明 問題 応用
平行四辺形 面積 求め方 対角線 720806-平行四辺形 面積 求め方 対角線
多角形の面積の求め方 長方形=縦×横 正方形=1辺×1辺=対角線×対角線÷2 平行四辺形=底辺×高さ 台形=(上底+下底)×高さ÷2 ひし形(対角線直交四角形)の面積=対角線×対角線÷2 三角形=底辺×高さ÷2 円の面積の求め方もとに面積の求め方を考えたり、公式をつくったりす る過程を重視しることが大切である」とある。次の 「ア 三角形や平行四辺形、ひし形及び台形の面積の 求め方」には、「三角形や平行四辺形、及び平行四辺形の対角線は中点で交わる 平行四辺形に対角線を引くと、2つの対角線が交わる点が、それぞれの対角線の中央にきます。 上記は平行四辺形の性質なので、是非理解しましょう。 平行四辺形の面積 平行四辺形の面積は、 底辺×高さ で計算します。
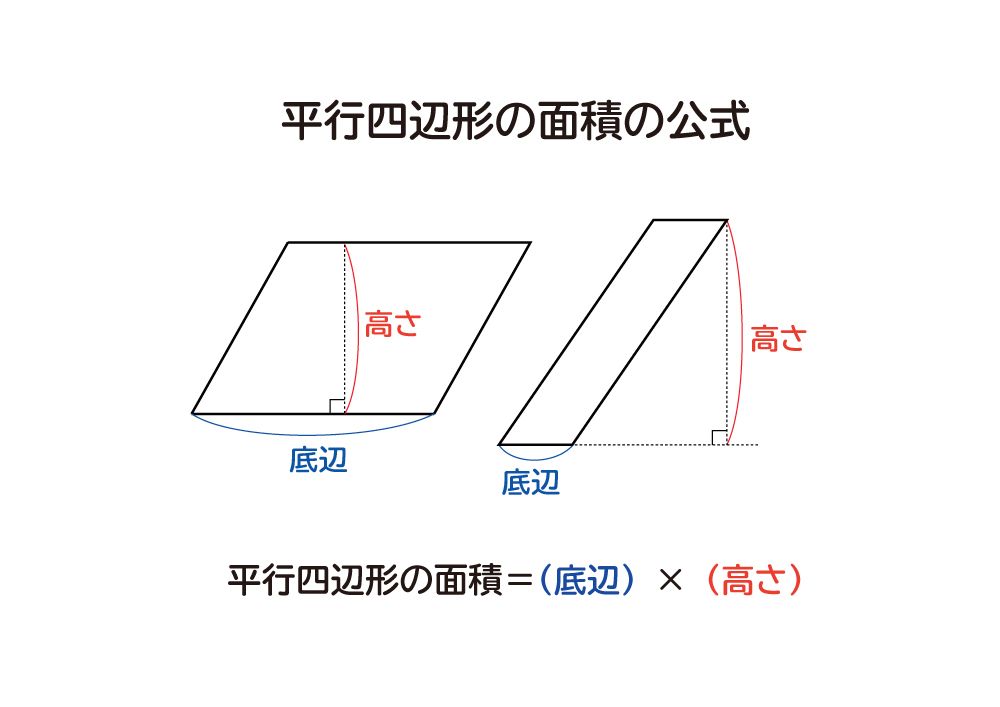
なぜ 平行四辺形の面積は 底辺 高さ なのか を説明します おかわりドリル
平行四辺形 面積 求め方 対角線
25 ++ 円錐 台 体積 求め 方 306122-円錐台 体積 求め方
円錐台の体積の求め方を覚えましょう ≪円錐台の体積の求め方≫ 図bのように円錐を作り、以下の式で答えを求めます。 (大きな円錐)-(小さい円錐)=円錐台 図b 図bを見ると、小さい円錐の高さ(〇㎝)と大きな円錐の高さ(〇+4㎝)を求めることが円錐の体積 円錐の体積は, V = 1 3πr2h V = 1 3 π r 2 h ( r r :半径, h h :高さ ) の公式で求めることができる. この公式は,円柱の体積の公式 V = πr2h V = π r 2 h に 1 3 1 3 をかけたものと考えることができるが,なぜ円柱の体積に 1 3 1 3 をかけることにより11月26日(火) 角錐の体積の求め方 6年生の算数の授業です。 角錐・円錐の体積の求め方には底面積×高さ÷3という公式があります。 「なぜ、÷3するのか」という疑問を解決するために、四角錐などの立体を組み合わせて考えました。 自分たちが体積を
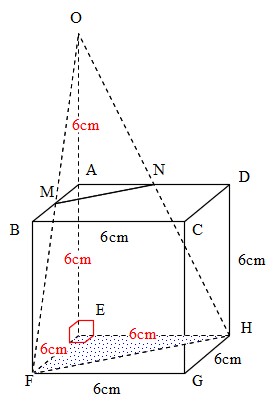
Mathematics 錐体の一部の体積 働きアリ
円錐台 体積 求め方
√1000以上 中3 数学 式の計算の利用 証明 208412-中3 数学 式の計算の利用 証明 図形
中学数学の式の計算の利用練習問題です。授業の予習、復習から定期テスト対策、受験勉強に活用してください。 次のことがらを証明しなさい。 中1数学の正負の数の計算問題 加法減法乗法除法、累乗、四則計算中学校3年式の計算の利用2/3時間・多項式16/18時間(東京書籍新しい数学3p29) 思考の開始 ・(道の面積) =(道幅)×(道の真ん中を通る円の周の長さ) ・道の面積は,道幅と道の真ん中を通る円の周の長さを かけると求まる。動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru

文字式を使った証明 展開 因数分解編 教遊者
